
【题目】已知方程![]() 只有一个实数根,则
只有一个实数根,则![]() 的取值范围是( )
的取值范围是( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() D.
D.![]() 或
或![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它可应用到有限维空间,并构成一般不动点定理的基石.布劳威尔不动点定理得名于荷兰数学家鲁伊兹·布劳威尔(L.E. J. Brouwer),简单的讲就是对于满足一定条件的连续函数![]() ,存在一个点
,存在一个点![]() ,使得
,使得![]() ,那么我们称该函数为“不动点”函数,下列为“不动点”函数的是( )
,那么我们称该函数为“不动点”函数,下列为“不动点”函数的是( )
A.![]() B.
B.![]()
C.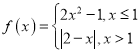 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国武汉于2019年10月18日至2019年10月27日成功举办了第七届世界军人运动会.来自109个国家的9300余名运动员同台竞技.经过激烈的角逐,奖牌榜的前3名如下:
国家 | 金牌 | 银牌 | 铜牌 | 奖牌总数 |
中国 | 133 | 64 | 42 | 239 |
俄罗斯 | 51 | 53 | 57 | 161 |
巴西 | 21 | 31 | 36 | 88 |
某数学爱好者采用分层抽样的方式,从中国和巴西获得金牌选手中抽取了22名获奖代表.从这22名中随机抽取3人, 则这3人中中国选手恰好1人的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC.
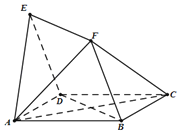
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:FC∥平面EAD;
(Ⅲ)求二面角A﹣FC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A-BCD中,平面ABC丄平面ADC, AD丄AC,AD=AC, ![]() ,若此三棱锥的外接球表面积为
,若此三棱锥的外接球表面积为![]() ,则三棱锥A-BCD体积的最大值为( )
,则三棱锥A-BCD体积的最大值为( )
A.7B.12C.6D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解该校某年级学生的阅读量(分钟),随机抽取了![]() 名学生调查一天的阅读时间,统计结果如下图表所示:
名学生调查一天的阅读时间,统计结果如下图表所示:
组号 | 分组 | 男生人数 | 男生人数占本组人数的频率 | 频率分布直方图 |
第1组 |
| 5 | 0.5 |
|
第2组 |
| 18 | 0.9 | |
第3组 |
| 27 | 0.9 | |
第4组 |
|
| 0.36 | |
第5组 |
| 3 | 0.2 |
(1)求出![]() 的值并估计该校学生一天的人均阅读时间;
的值并估计该校学生一天的人均阅读时间;
(2)一天的阅读时间不少于35分钟称为“喜好阅读者”.根据以上数据,完成下面的![]() 列联表,并回答能否在犯错误的概率不超过0.05的前提下认为“喜好阅读者”与“性别”有关?
列联表,并回答能否在犯错误的概率不超过0.05的前提下认为“喜好阅读者”与“性别”有关?
喜好阅读者 | 非喜好阅读者 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: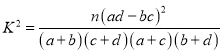 (其中
(其中![]() 为样本容量).
为样本容量).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com