
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为函数f(x)的不动点.已知f(x)=x2+bx+c
(1)若f(x)有两个不动点为﹣3,2,求函数y=f(x)的零点?
(2)若c= ![]() 时,函数f(x)没有不动点,求实数b的取值范围?
时,函数f(x)没有不动点,求实数b的取值范围?
科目:高中数学 来源: 题型:
【题目】设过原点 O 的直线与圆 C : ![]() 的一个交点为 P ,点 M 为线段 OP 的中点。
的一个交点为 P ,点 M 为线段 OP 的中点。
(1)求圆 C 的极坐标方程;
(2)求点 M 轨迹的极坐标方程,并说明它是什么曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)= ![]() (a∈R)是奇函数,函数g(x)=
(a∈R)是奇函数,函数g(x)= ![]() 的定义域为(﹣1,+∞).
的定义域为(﹣1,+∞).
(1)求a的值;
(2)若g(x)= ![]() 在(﹣1,+∞)上递减,根据单调性的定义求实数m的取值范围;
在(﹣1,+∞)上递减,根据单调性的定义求实数m的取值范围;
(3)在(2)的条件下,若函数h(x)=f(x)+g(x)在区间(﹣1,1)上有且仅有两个不同的零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)为奇函数,当x≥0时,f(x)= ![]() .g(x)=
.g(x)= ![]() ,
,
(1)求当x<0时,函数f(x)的解析式;
(2)求g(x)的解析式,并证明g(x)的奇偶性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
附: ![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
(1)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中恰有2个人接受挑战的概率是多少?
(2)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构进行了随机抽样调查,调查得到如下 ![]() 列联表:
列联表:
接受挑战 | 不接受挑战 | 合计 | |
男性 | 50 | 10 | 60 |
女性 | 25 | 15 | 40 |
合计 | 75 | 25 | 100 |
根据表中数据,是否有99%的把握认为“冰桶挑战赛与受邀者的性别有关”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
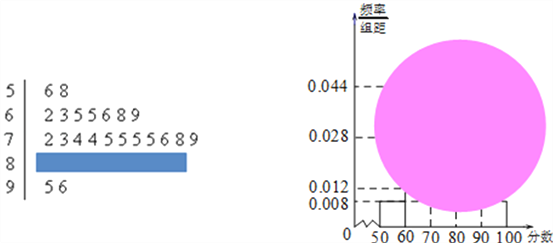
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
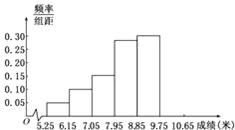
【题目】某市为了了解今年高中毕业生的体能状况,从本市某校高中毕业班中抽取一个班进行铅球测试,成绩在8.0米(精确到0.1米)以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30.第6小组的频数是7.
(1)求这次铅球测试成绩合格的人数;
(2)若由直方图来估计这组数据的中位数,指出它在第几组内,并说明理由;
(3)若参加此次测试的学生中,有9人的成绩为优秀,现在要从成绩优秀的学生中,随机选出2人参加“毕业运动会”,已知a、b的成绩均为优秀,求两人至少有1人入选的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一大学生自主创业,拟生产并销售某电子产品![]() 万件(生产量与销售量相等),为扩大影响进行促销,促销费用
万件(生产量与销售量相等),为扩大影响进行促销,促销费用![]() (万元)满足
(万元)满足![]() (其中
(其中![]() 为正常数).已知生产该产品还需投入成本
为正常数).已知生产该产品还需投入成本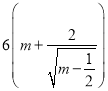 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 元/件.
元/件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,此大学生所获利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com