
【题目】在棱长为2的正方体![]() 中,点
中,点![]() 是正方体棱上一点,
是正方体棱上一点,![]() .
.
①若![]() ,则满足条件的点
,则满足条件的点![]() 的个数为______;
的个数为______;
②若满足![]() 的点
的点![]() 的个数为6,则
的个数为6,则![]() 的取值范围是______.
的取值范围是______.
【答案】4 ![]()
【解析】
(1)由题意可得点![]() 是以
是以![]() 为焦距,以
为焦距,以![]() 为长半轴的椭圆与正方体与棱的交点,可求解;
为长半轴的椭圆与正方体与棱的交点,可求解;
(2)利用三角形两边之和大于第三边,以及点![]() 的个数为6个时,短半轴范围,即可求解.
的个数为6个时,短半轴范围,即可求解.
(1)正方体的棱长为![]() ,
,
![]() 是以
是以![]() 为焦距,以
为焦距,以![]() 为长半轴的椭圆,
为长半轴的椭圆,
![]() 在正方体的棱上,
在正方体的棱上,![]() 应是椭圆与正方体与棱的交点,
应是椭圆与正方体与棱的交点,
结合正方体的性质可得,满足条件的点为![]() ,
,
以及棱![]() 各有一点满足条件,
各有一点满足条件,
故满足条件的点![]() 的个数为
的个数为![]() ;
;
(2)![]() ,
,
当椭圆短半轴![]() 时,椭圆与棱
时,椭圆与棱![]() ,
,![]()
各有一个交点,与其它棱无交点,满足题意,
![]()
当![]() 时,
时,![]() 由(1)得不合题意.
由(1)得不合题意.
当![]() 时,根据正方体的性质,
时,根据正方体的性质,
至多只有4个点在棱上,不合题意;
当![]() 时,椭圆与棱
时,椭圆与棱![]()
各有一个交点,满足题意,![]() ,
,
![]() ;
;
当![]() ,椭圆至多与正方体的棱有4个交点,不合题意.
,椭圆至多与正方体的棱有4个交点,不合题意.
综上 ![]() 或
或![]() .
.
故答案为:(1)4;(2)![]()


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某工厂有甲,乙两个车间生产同一种产品,甲车间有工人![]() 人,乙车间有工人
人,乙车间有工人![]() 人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:
人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:![]() )进行统计,按照
)进行统计,按照![]() 进行分组,得到下列统计图.
进行分组,得到下列统计图.
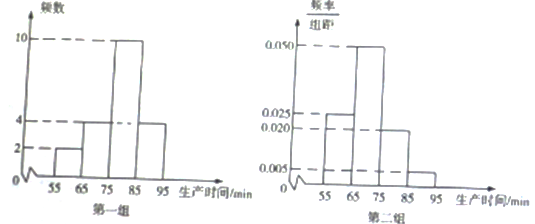
![]() 分别估算两个车间工人中,生产一件产品时间少于
分别估算两个车间工人中,生产一件产品时间少于![]() 的人数;
的人数;
![]() 分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
分别估计两个车间工人生产一件产品时间的平均值,并推测车哪个车间工人的生产效率更高?
![]() 从第一组生产时间少于
从第一组生产时间少于![]() 的工人中随机抽取
的工人中随机抽取![]() 人,求抽取
人,求抽取![]() 人中,至少
人中,至少![]() 人生产时间少于
人生产时间少于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,
中,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() :
:
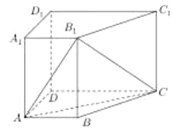
(1)求证:![]() 平面
平面![]() ;
;
(2)现将与四棱柱![]() 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为![]() ,写出
,写出![]() 的解析式;(直接写出答案,不必说明理由)
的解析式;(直接写出答案,不必说明理由)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点P(4,0),且在y轴上截得的弦MN的长为8.
(1)求动圆圆心C的轨迹方程;
(2)过点(2,0)的直线l与动圆圆心C的轨迹交于A,B两点,求证:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】苹果可按果径![]() (最大横切面直径,单位:
(最大横切面直径,单位:![]() .)分为五个等级:
.)分为五个等级:![]() 时为1级,
时为1级,![]() 时为2级,
时为2级,![]() 时为3级,
时为3级,![]() 时为4级,
时为4级,![]() 时为5级.不同果径的苹果,按照不同外观指标又分为特级果、一级果、二级果.某果园采摘苹果10000个,果径
时为5级.不同果径的苹果,按照不同外观指标又分为特级果、一级果、二级果.某果园采摘苹果10000个,果径![]() 均在
均在![]() 内,从中随机抽取2000个苹果进行统计分析,得到如图1所示的频率分布直方图,图2为抽取的样本中果径在80以上的苹果的等级分布统计图.
内,从中随机抽取2000个苹果进行统计分析,得到如图1所示的频率分布直方图,图2为抽取的样本中果径在80以上的苹果的等级分布统计图.
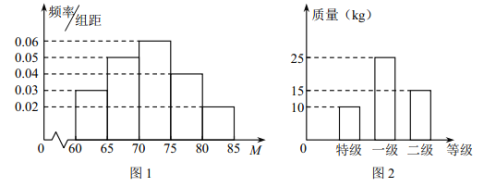
(1)假设![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 的近似值为果径的样本平均数
的近似值为果径的样本平均数![]() (同一组数据用该区间的中点值代替),
(同一组数据用该区间的中点值代替),![]() ,试估计采摘的10000个苹果中,果径
,试估计采摘的10000个苹果中,果径![]() 位于区间
位于区间![]() 的苹果个数;
的苹果个数;
(2)已知该果园今年共收获果径在80以上的苹果![]() ,且售价为特级果12元
,且售价为特级果12元![]() ,一级果10元
,一级果10元![]() ,二级果9元
,二级果9元![]() .设该果园售出这
.设该果园售出这![]() 苹果的收入为
苹果的收入为![]() ,以频率估计概率,求
,以频率估计概率,求![]() 的数学期望.
的数学期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则
![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,A为圆O1上任意一点,点D在线段
,A为圆O1上任意一点,点D在线段![]() 上.
上.![]() ,已知
,已知![]() ,
,![]() .
.
(1)求点D的轨迹方程H;
(2)若直线![]() 与方程H所表示的图像交于E,F两点,
与方程H所表示的图像交于E,F两点,![]() 是椭圆
是椭圆![]() 上任意一点.若OG平分弦EF,且
上任意一点.若OG平分弦EF,且![]() ,
,![]() ,试判断四边形OEGF形状并证明.
,试判断四边形OEGF形状并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着电子商务的兴起,网上销售为人们带来了诸多便利.商务部预计,到2020年,网络销售占比将达到![]() .网购的发展同时促进了快递业的发展,现有甲、乙两个快递公司,每位打包工平均每天打包数量在
.网购的发展同时促进了快递业的发展,现有甲、乙两个快递公司,每位打包工平均每天打包数量在![]() 范围内.为扩展业务,现招聘打包工.两公司提供的工资方案如下:甲公司打包工每天基础工资64元,且每天每打包一件快递另赚1元;乙公司打包工无基础工资,如果每天打包量不超过240件,则每打包一件快递可赚1.2元;如果当天打包量超过240件,则超出的部分每件赚1.8元.
范围内.为扩展业务,现招聘打包工.两公司提供的工资方案如下:甲公司打包工每天基础工资64元,且每天每打包一件快递另赚1元;乙公司打包工无基础工资,如果每天打包量不超过240件,则每打包一件快递可赚1.2元;如果当天打包量超过240件,则超出的部分每件赚1.8元.
下图为随机抽取的打包工每天需要打包数量的频率分布直方图,以打包量的频率作为各打包量发生的概率.(同一组中的数据用该组区间的中间值作代表).
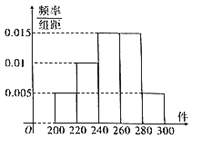
(1)(i)以每天打包量为自变量![]() ,写出乙公司打包工的收入函数
,写出乙公司打包工的收入函数![]() ;
;
(ii)若打包工小李是乙公司员工,求小李一天收入不低于324元的概率;
(2)某打包工在甲、乙两个快递公司中选择一个公司工作,如果仅从日平均收入的角度考虑,请利用所学的统计学知识为该打包工作出选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com