
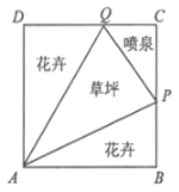
【题目】如图所示,我市某居民小区拟在边长为1百米的正方形地块![]() 上划出一个三角形地块
上划出一个三角形地块![]() 种植草坪,两个三角形地块
种植草坪,两个三角形地块![]() 与
与![]() 种植花卉,一个三角形地块
种植花卉,一个三角形地块![]() 设计成水景喷泉,四周铺设小路供居民平时休闲散步,点
设计成水景喷泉,四周铺设小路供居民平时休闲散步,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,记
上,记![]() .
.
(1)当![]() 时,求花卉种植面积
时,求花卉种植面积![]() 关于
关于![]() 的函数表达式,并求
的函数表达式,并求![]() 的最小值;
的最小值;
(2)考虑到小区道路的整体规划,要求![]() ,请探究
,请探究![]() 是否为定值,若是,求出此定值,若不是,请说明理由.
是否为定值,若是,求出此定值,若不是,请说明理由.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,椭圆
,椭圆![]() 上短轴的一个端点与两个焦点构成的三角形的面积为
上短轴的一个端点与两个焦点构成的三角形的面积为![]() ;
;
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在第二象限),
在第二象限),![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点,若
两侧的动点,若![]() ,求证:直线
,求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市推行“共享汽车”服务,租用汽车按行驶里程加用车时间收费,标准是“1元/公里+0.2元/分钟”,刚在该市参加工作的小刘拟租用“共享汽车“上下班.单位同事老李告诉他:“上下班往返总路程虽然只有10公里,但偶尔上下班总共也需要用时大约1小时”,并将自己近50天往返开车的花费时间情况统计如下
时间(分钟) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
次数ξ | 8 | 18 | 14 | 8 | 2 |
将老李统计的各时间段频率视为相应概率,假定往返的路况不变,而且每次路上开车花费时间视为用车时间.
(1)试估计小刘每天平均支付的租车费用(每个时间段以中点时间计算);
(2)小刘认为只要上下班开车总用时不超过45分钟,租用“共享汽车”为他该日的“最优选择”,小刘拟租用该车上下班2天,设其中有ξ天为“最优选择”,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的一个焦点
)的一个焦点![]() 与抛物线
与抛物线![]() :
:![]() 的焦点重合,且离心率为
的焦点重合,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过焦点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,满足
两点,满足![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(![]() ),把函数f(x)的图象向左平移
),把函数f(x)的图象向左平移![]() 个单位得函数g(x)的图象,则下面结论正确的是( )
个单位得函数g(x)的图象,则下面结论正确的是( )
A.函数g(x)是偶函数
B.函数g(x)的最小正周期是4π
C.函数g(x)在区间[π,3π]上是增区数
D.函数g(x)的图象关于直线x=π对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆![]() :
:![]() 上有一动点
上有一动点![]() ,
,![]() 到椭圆
到椭圆![]() 的两焦点
的两焦点![]() ,
,![]() 的距离之和等于
的距离之和等于![]() ,
,![]() 到直线
到直线![]() 的最大距离为
的最大距离为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 、
、![]() ,
,![]() (
(![]() 为坐标原点)且
为坐标原点)且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com