
【题目】如图,有一壁画,最高点A处离地面AO=4m,最低点B处离地面BO=2m,观赏它的C点在过墙角O点与地面成30°角的射线上. 
(1)设点C到墙的距离为x,当x= ![]() m时,求tanθ的值;
m时,求tanθ的值;
(2)问C点离墙多远时,视角θ最大?
科目:高中数学 来源: 题型:
【题目】二项式![]() 的展开式中只有第6项的二项式系数最大,且展开式中的第3项的系数是第4项的系数的3倍,则
的展开式中只有第6项的二项式系数最大,且展开式中的第3项的系数是第4项的系数的3倍,则![]() 的值为( )
的值为( )
A. 4 B. 8 C. 12 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(18)(本小题满分12分)在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙中心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,A6和4名B1,B2,
B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示。
(I)求接受甲种心理暗示的志愿者中包含A1但不包含B3的频率。
(II)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中![]() 轴的正半轴重合.若曲线
轴的正半轴重合.若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为极坐标方程;
的参数方程化为极坐标方程;
(2)由直线![]() 上一点向曲线
上一点向曲线![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和Sn=2n+r.
(1)求实数r的值和{an}的通项公式;
(2)若数列{bn}满足b1=1,bn+1﹣bn=log2an+1 , 求bn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在多面体![]() 中,
中, ![]() 与
与![]() 均为边长为2的正方形,
均为边长为2的正方形, ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额(单位:百万元)之间有如下对应数据:
如果y与x之间具有线性相关关系.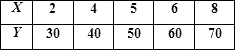
(1)作出这些数据的散点图;
(2)求这些数据的线性回归方程;
(3)预测当广告费支出为9百万元时的销售额.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com