
【题目】某物流公司每天从甲地运货物到乙地,统计最近的200次可配送的货物量,可得可配送的货物量的频率分布直方图,所图所示,回答以下问题(直方图中每个小组取中间值作为该组数据的替代值).
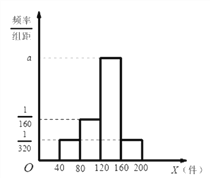
(1)求该物流公司每天从甲地到乙地平均可配送的货物量;
(2)该物流公司拟购置货车专门运营从甲地到乙地的货物,一辆货车每天只能运营一趟,每辆车每趟最多只能装载40件货物,满载发车,否则不发车.若发车,则每辆车每趟可获利1000元;若未发车,则每辆车每天平均亏损200元.为使该物流公司此项业务的营业利润最大,该物流公司应该购置几辆货车?
【答案】(1)125 (2) 3趟车
【解析】
试题分析:(1)由频率分布直方图的几何意义求出a的值,进而可得每组的频率,则可得![]() ;(2)由(1)可知从甲地到乙地的客流量在60,100,140,180的次数分别为25,50,100,25,依题意,讨论发发1趟车、2趟车、3趟车、4趟车,根据发车所获得的利润,求出每1种情况的平均利润即可.
;(2)由(1)可知从甲地到乙地的客流量在60,100,140,180的次数分别为25,50,100,25,依题意,讨论发发1趟车、2趟车、3趟车、4趟车,根据发车所获得的利润,求出每1种情况的平均利润即可.
试题解析:
(1)在区间![]() 的频率为
的频率为![]() ,
,
从甲地到乙地的客流量在![]() 的所占频率分别为
的所占频率分别为![]() .
.
从甲地到乙地的客流量在60,100,140,180的次数分别为25,50,100,25.
从甲地到乙地每天的平均客流量为:
![]() .
.
(2)由(1)可知从甲地到乙地的客流量在60,100,140,180的次数分别为25,50,100,25,依题意
(i)若发1趟车,则运输公司每天的营业利润值为1000;
(ii)若发2趟车,则每天的营业利润值的可能取值为2000,800,其次数分别为175,25
故平均利润值为![]() ;
;
(iii)若发3趟车,则每天的营业利润值的可能取值为3000,1800,600,其次数分别为125,50,25
故平均利润值为![]() ;
;
(iiii)若发4趟车,则每天的营业利润值的可能取值为4000,2800,1600,400其次数分别为25,100,50,25,
故平均利润值为![]() ;
;
因为2400>2350>1850>1000,
所以为使运输公司每天的营业利润最大,该公司每天应该发3趟车.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】某湿地公园内有一条河,现打算建一座桥将河两岸的路连接起来,剖面设计图纸如下:

其中,点![]() 为
为![]() 轴上关于原点对称的两点,曲线段
轴上关于原点对称的两点,曲线段![]() 是桥的主体,
是桥的主体,![]() 为桥顶,且曲线段
为桥顶,且曲线段![]() 在图纸上的图形对应函数的解析式为
在图纸上的图形对应函数的解析式为![]() ,曲线段
,曲线段![]() 均为开口向上的抛物线段,且
均为开口向上的抛物线段,且![]() 分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(
分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(![]() )的切线的斜率相等.
)的切线的斜率相等.
(1)求曲线段![]() 在图纸上对应函数的解析式,并写出定义域;
在图纸上对应函数的解析式,并写出定义域;
(2)车辆从![]() 经
经![]() 倒
倒![]() 爬坡,定义车辆上桥过程中某点
爬坡,定义车辆上桥过程中某点![]() 所需要的爬坡能力为:
所需要的爬坡能力为:![]() (该点
(该点![]() 与桥顶间的水平距离)
与桥顶间的水平距离)![]() (设计图纸上该点处的切线的斜率),其中
(设计图纸上该点处的切线的斜率),其中![]() 的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为
的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为![]() 米,
米,![]() 米,
米,![]() 米,又已知图纸上一个单位长度表示实际长度
米,又已知图纸上一个单位长度表示实际长度![]() 米,试问三种类型的观光车是否都可以顺利过桥?
米,试问三种类型的观光车是否都可以顺利过桥?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量按照其质量指标值M进行等级划分,具体如下表:
质量指标值M |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
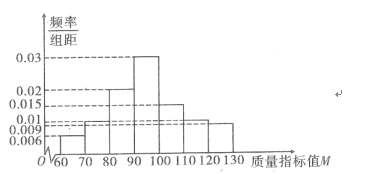
现从某企业生产的这种产品中随机抽取了100件作为样本,对其质量指标值M进行统计分析,得到如图所示的频率分布直方图.
(1)记A表示事件“一件这种产品为二等品或一等品”,试估计事件A的概率;
(2)已知该企业的这种产品每件一等品、二等品、三等品的利润分别为10元、6元、2元,试估计该企业销售10000件该产品的利润;
(3)根据该产品质量指标值M的频率分布直方图,求质量指标值M的中位数的估计值(精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是椭圆
是椭圆![]()
![]() 的四个顶点,菱形
的四个顶点,菱形![]() 的面积与其内切圆面积分别为
的面积与其内切圆面积分别为![]() ,
, ![]() .椭圆
.椭圆![]() 的内接
的内接![]() 的重心(三条中线的交点)为坐标原点
的重心(三条中线的交点)为坐标原点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2) ![]() 的面积是否为定值?若是,求出该定值,若不是,请说明理由.
的面积是否为定值?若是,求出该定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在印度有一个古老的传说:舍罕王打算奖赏国际象棋的发明人一宰相西萨·班·达依尔.国王问他想要什么,他对国王说:“陛下,请您在这张棋盘的第1个小格里,赏给我1粒麦子,在第2个小格里给2粒,第3小格给4粒,以后每1小格都比前1小格加1倍.请您把这样摆满棋盘上所有的64格的麦粒,都赏给您的仆人吧!”国王觉得这要求太容易满足了,就同意给他这些麦粒.当人们把一袋一袋的麦子搬来开始计数时,国王才发现就是把全印度甚至全世界的麦粒全拿来,也满足不了那位宰相的要求.那么,宰相要求得到的麦粒到底有多少粒?如图所示的程序框图是为了计算上面这个问题而设计的,那么在“![]() ”和“
”和“![]() ”中,可以先后填入( )
”中,可以先后填入( )
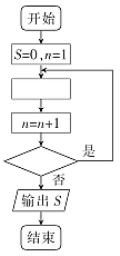
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com