
【题目】已知函数f(x)=lnx+ ![]() ax2﹣2x存在单调递减区间,则实数a的取值范围为 .
ax2﹣2x存在单调递减区间,则实数a的取值范围为 .
【答案】(﹣∞,1)
【解析】解:对函数求导数,得f′(x)= ![]() ,(x>0)
,(x>0)
依题意,得f′(x)<0在(0,+∞)上有解.即ax2﹣2x+1<0在x>0时有解.①显然a≤0时,不等式有解,②a>0时,只需a< ![]() 在x>0有解,
在x>0有解,
即只需a< ![]() ,
,
令g(x)= ![]() ,g(x)在(0,1)递增,在(1,+∞)递减,
,g(x)在(0,1)递增,在(1,+∞)递减,
∴g(x)最大值=g(1)=1,
∴a<1,
综合①②得a<1,
所以答案是:(﹣∞,1).
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】如图,多面体PABCD的直观图及三视图如图所示,E、F分别为PC、BD的中点.

(I)求证:EF∥平面PAD;
(II)求证:平面PDC⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的首项a1=1,且(n+1)a ![]() +anan+1﹣na
+anan+1﹣na ![]() =0对n∈N*都成立.
=0对n∈N*都成立.
(1)求{an}的通项公式;
(2)记bn=a2n﹣1a2n+1 , 数列{bn}的前n项和为Tn , 证明:Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)图象上不同两点A(x1 , y1),B(x2 , y2)处的切线的斜率分别是kA , kB , 规定φ(A,B)= ![]() (|AB|为线段AB的长度)叫做曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: ①函数y=x3图象上两点A与B的横坐标分别为1和﹣1,则φ(A,B)=0;
(|AB|为线段AB的长度)叫做曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: ①函数y=x3图象上两点A与B的横坐标分别为1和﹣1,则φ(A,B)=0;
②存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
③设点A,B是抛物线y=x2+1上不同的两点,则φ(A,B)≤2;
④设曲线y=ex(e是自然对数的底数)上不同两点A(x1 , y1),B(x2 , y2),则φ(A,B)<1.
其中真命题的序号为 . (将所有真命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=lnx+ ![]() ,g(x)=ex﹣
,g(x)=ex﹣ ![]() (e是自然对数的底数,a∈R).
(e是自然对数的底数,a∈R).
(Ⅰ)求证:|f(x)|≥﹣(x﹣1)2+ ![]() ;
;
(Ⅱ)已知[x]表示不超过x的最大整数,如[1.9]=1,[﹣2.1]=﹣3,若对任意x1≥0,都存在x2>0,使得g(x1)≥[f(x2)]成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为U=(0,+![]() ),且满足条件f(4)=1。对任意的x1,x2∈U,有f(x1·x2)=f(x1)+f(x2),且当x1≠x2时,有
),且满足条件f(4)=1。对任意的x1,x2∈U,有f(x1·x2)=f(x1)+f(x2),且当x1≠x2时,有![]() >0。
>0。
(1)求f(1)的值;
(2)如果f(x+6)+f(x)>2,求x的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为招聘新员工设计了一个面试方案:应聘者从6道备选题中一次性随机抽取3道题,按照题目要求独立完成.规定:至少正确完成其中2道题的便可通过.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是 ![]() ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(Ⅰ)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(Ⅱ)请分析比较甲、乙两人谁的面试通过的可能性大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该市决定在第3,4组的志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率. 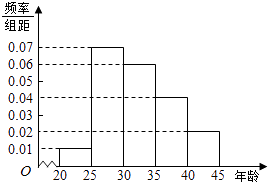
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com