
 是公差不等于0的等差数列,
是公差不等于0的等差数列,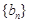 是等比数列
是等比数列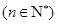 ,且
,且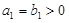 .
.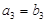 ,比较
,比较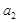 与
与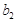 的大小关系;
的大小关系;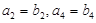 .(ⅰ)判断
.(ⅰ)判断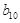 是否为数列
是否为数列 中的某一项,并请说明理由;
中的某一项,并请说明理由;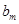 是数列
是数列 中的某一项,写出正整数
中的某一项,写出正整数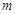 的集合(不必说明理由).
的集合(不必说明理由).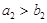 ,(2)
,(2)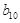 是
是 中的一项,正整数
中的一项,正整数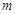 的集合是
的集合是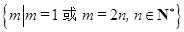 .
. 的
的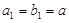 ,
, 公差为
公差为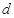 ,
,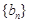 公比为
公比为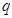 ,由
,由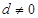 ,得
,得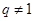 ,比较
,比较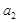 与
与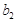 的大小关系,由已知
的大小关系,由已知 是公差不等于0的等差数列,
是公差不等于0的等差数列,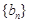 是等比数列
是等比数列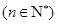 ,且
,且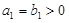 ,且
,且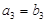 ,得
,得 ,
,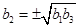 ,当
,当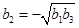 时,显然
时,显然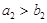 ,当
,当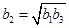 时,由平均值不等式
时,由平均值不等式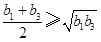 ,从而可比较
,从而可比较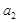 与
与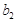 的大小关系;(2)若
的大小关系;(2)若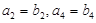 ,可得
,可得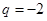 ,
,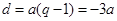 ,(ⅰ)令
,(ⅰ)令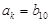 ,由等差数列,等比数列的通项公式,建立方程,解出
,由等差数列,等比数列的通项公式,建立方程,解出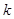 ,若是正整数,
,若是正整数,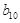 为数列
为数列 中的某一项,若不是正整数,
中的某一项,若不是正整数,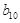 不是数列
不是数列 中的一项,(ⅱ)若
中的一项,(ⅱ)若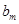 是数列
是数列 中的某一项,写出正整数
中的某一项,写出正整数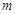 的集合,可由(ⅰ)的方法写出.
的集合,可由(ⅰ)的方法写出. 的
的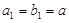 ,
, 公差为
公差为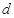 ,
,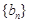 公比为
公比为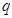 ,由
,由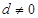 ,得
,得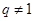
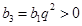 ,
, ,
,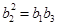 ,
,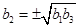 ,
,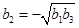 时,显然
时,显然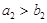 ;
;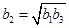 时,由平均值不等式
时,由平均值不等式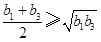 ,当且仅当
,当且仅当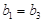 时取等号,而
时取等号,而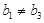 ,所以
,所以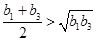 即
即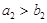 .综上所述,
.综上所述,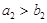 . 5分
. 5分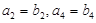 ,所以
,所以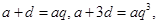 得
得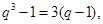 所以
所以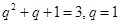 或
或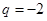 .因为
.因为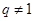 ,所以
,所以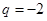 ,
,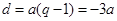 .
.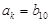 ,即
,即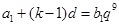 ,
,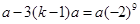 ,
,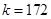 ,所以
,所以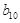 是
是 中的一项.
中的一项.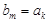 ,则
,则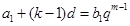 ,
,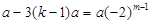 ,
,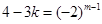
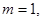 或
或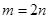 ,(
,(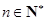 )时,
)时,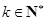 .
.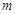 的集合是
的集合是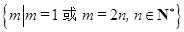 . 13分
. 13分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com