
【题目】某创业投资公司拟投资开发某种新能源产品,估计能获得10万元到1 000万元的投资收益.现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金不超过投资收益的20%.
(1)请分析函数y= ![]() +1是否符合公司要求的奖励函数模型,并说明原因;
+1是否符合公司要求的奖励函数模型,并说明原因;
(2)若该公司采用函数模型y= ![]() 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值.
【答案】
(1)解:对于函数模型y=f(x)= ![]() +1,
+1,
当x∈[10,1 000]时,f(x)为增函数,
f(x)max=f(1 000)= ![]() +1=
+1= ![]() +1<9,所以f(x)≤9恒成立,
+1<9,所以f(x)≤9恒成立,
又因为当x∈[10,1 000]时f(x)﹣ ![]() =﹣
=﹣ ![]() +1≤f(10)=﹣
+1≤f(10)=﹣ ![]() <0,
<0,
所以f(x)≤ ![]() 恒成立,
恒成立,
故函数模型y= ![]() -3+1符合公司要求
-3+1符合公司要求
(2)解:对于函数模型y=g(x)= ![]() ,即g(x)=10﹣
,即g(x)=10﹣ ![]() ,
,
当3a+20>0,即a>﹣ ![]() 时递增,
时递增,
为使g(x)≤9对于x∈[10,1 000]恒成立,
即要g(1 000)≤9,3a+18≥1 000,即a≥ ![]() ,
,
为使g(x)≤ ![]() 对于x∈[10,1 000]恒成立,
对于x∈[10,1 000]恒成立,
即要 ![]() ≤5,即x2﹣48x+15a≥0恒成立,
≤5,即x2﹣48x+15a≥0恒成立,
即(x﹣24)2+15a﹣576≥0(x∈[10,1 000])恒成立,又24∈[10,1 000],
故只需15a﹣576≥0即可,
所以a≥ ![]() .
.
综上,a≥ ![]() ,故最小的正整数a的值为328
,故最小的正整数a的值为328
【解析】(1)设奖励函数模型为y=f(x),根据“奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,说明在定义域上是增函数,且奖金不超过9万元,即f(x)≤9,同时奖金不超过投资收益的20%.即f(x)≤ ![]() .(2)先将函数解析式进行化简,然后根据函数的单调性,以及使g(x)≤9对x∈[10,1000]恒成立以及使g(x)≤
.(2)先将函数解析式进行化简,然后根据函数的单调性,以及使g(x)≤9对x∈[10,1000]恒成立以及使g(x)≤ ![]() 对x∈[10,1000]恒成立,建立不等式,求出相应的a的取值范围.
对x∈[10,1000]恒成立,建立不等式,求出相应的a的取值范围.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】孝感星河天街购物广场某营销部门随机抽查了100名市民在2017年国庆长假期间购物广场的消费金额,所得数据如表,已知消费金额不超过3千元与超过3千元的人数比恰为3:2.
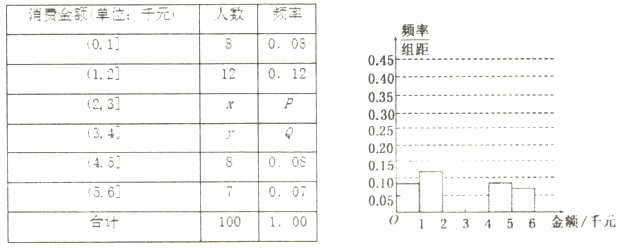
(1)试确定![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值,并补全频率分布直方图(如图);
的值,并补全频率分布直方图(如图);
(2)用分层抽样的方法从消费金额在![]() 和
和![]() 的两个群体中抽取5人进行问卷调查,则各小组应抽取几人?若从这5人中随机选取2人,则此2人来自同一群体的概率是多少?
的两个群体中抽取5人进行问卷调查,则各小组应抽取几人?若从这5人中随机选取2人,则此2人来自同一群体的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() :
: ![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,且椭圆的长轴长为4.
的离心率互为倒数,且椭圆的长轴长为4.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() (
(![]() )为椭圆
)为椭圆![]() 上一点,求
上一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孝感车天地关于某品牌汽车的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (千元)由如表的统计资料:
(千元)由如表的统计资料:
| 2 | 3 | 4 | 5 | 6 |
| 2.1 | 3.4 | 5.9 | 6.6 | 7.0 |
(1)画出散点图并判断使用年限与所支出的维修费用是否线性相关;如果线性相关,求回归直线方程;
(2)若使用超过8年,维修费用超过1.5万元时,车主将处理掉该车,估计第10年年底时,车主是否会处理掉该车?
(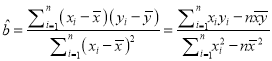 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x﹣1.
(1)求f(x)的函数解析式;
(2)作出函数f(x)的简图,写出函数f(x)的单调减区间及最值.
(3)若关于x的方程f(x)=m有两个解,试说出实数m的取值范围.(只要写出结果,不用给出证明过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的点80%,求![]() 的值;
的值;
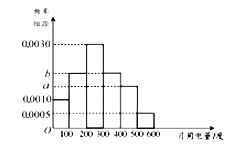
(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的通项为an , 前n项和为sn , 且an是sn与2的等差中项,数列{bn}中,b1=1,点P(bn , bn+1)在直线x﹣y+2=0上. (Ⅰ)求数列{an}、{bn}的通项公式an , bn
(Ⅱ)设{bn}的前n项和为Bn , 试比较 ![]() 与2的大小.
与2的大小.
(Ⅲ)设Tn= ![]() ,若对一切正整数n,Tn<c(c∈Z)恒成立,求c的最小值.
,若对一切正整数n,Tn<c(c∈Z)恒成立,求c的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com