
【题目】(1)证明:![]() ;
;
(2)证明:对任何正整数n,存在多项式函数![]() ,使得
,使得![]() 对所有实数x均成立,其中
对所有实数x均成立,其中![]() 均为整数,当n为奇数时,
均为整数,当n为奇数时,![]() ,当n为偶数时,
,当n为偶数时,![]() ;
;
(3)利用(2)的结论判断![]() 是否为有理数?
是否为有理数?
【答案】(1)见解析;(2)见解析;(3)不是
【解析】
(1)![]() ,利用两角和的正弦和二倍角公式,进行证明;(2)对
,利用两角和的正弦和二倍角公式,进行证明;(2)对![]() 分奇偶,即
分奇偶,即![]() 和
和![]() 两种情况,结合两角和的余弦公式,积化和差公式,利用数学归纳法进行证明;(3)根据(2)的结论,将
两种情况,结合两角和的余弦公式,积化和差公式,利用数学归纳法进行证明;(3)根据(2)的结论,将![]() 表示出来,然后判断其每一项都为无理数,从而得到答案.
表示出来,然后判断其每一项都为无理数,从而得到答案.
(1)![]()
![]()
![]()
![]()
所以原式得证.
(2)![]() 为奇数时,
为奇数时,
![]() 时,
时,![]() ,其中
,其中![]() ,成立
,成立
![]() 时,
时,![]()
![]() ,其中
,其中![]() ,成立
,成立
![]() 时,
时,![]()
![]() ,其中
,其中![]() ,成立,
,成立,
则当![]() 时,
时,
![]()
![]()
所以得到
![]()
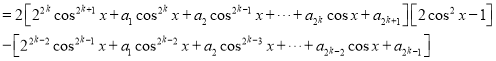
![]()
因为![]() 均为整数,所以
均为整数,所以![]() 也均为整数,
也均为整数,
故原式成立;
![]() 为偶数时,
为偶数时,
![]() 时,
时,![]() ,其中
,其中![]() ,
,
![]() 时,
时,![]()
![]() ,
,
其中![]() ,成立,
,成立,
![]() 时,
时,![]()
![]() ,
,
其中![]() ,成立,
,成立,
则当![]() 时,
时,
![]()
![]()
所以得到
![]()

![]() 其中
其中![]() ,
,
因为![]() 均为整数,所以
均为整数,所以![]() 也均为整数,
也均为整数,
故原式成立;
综上可得:对任何正整数![]() ,存在多项式函数
,存在多项式函数![]() ,使得
,使得![]() 对所有实数
对所有实数![]() 均成立,其中
均成立,其中![]() ,
,![]() 均为整数,当
均为整数,当![]() 为奇数时,
为奇数时,![]() ,当
,当![]() 为偶数时,
为偶数时,![]() ;
;
(3)由(2)可得![]()
![]()
![]()
![]()
其中![]() 均为有理数,
均为有理数,
因为![]() 为无理数,所以
为无理数,所以![]() 均为无理数,
均为无理数,
故![]() 为无理数,
为无理数,
所以![]() 不是有理数.
不是有理数.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高 气温 | [10, 15) | [15, 20) | [20, 25) | [25, 30) | [30, 35) | [35, 40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列.
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在几何体ABCDE中,AB⊥平面BCE,且△BCE是正三角形,四边形ABCD为正方形,F是线段CD上的中点,G是线段BE的中点,且AB=2.
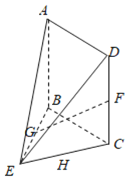
(1)求证:GF∥平面ADE;
(2)求三棱锥F–BGC的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点 .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过椭圆![]() 的左焦点的直线
的左焦点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 过坐标原点且与直线
过坐标原点且与直线![]() 的斜率互为相反数.若直线
的斜率互为相反数.若直线![]() 与椭圆交于
与椭圆交于![]() 两点且均不与点
两点且均不与点![]() 重合,设直线
重合,设直线![]() 与
与![]() 轴所成的锐角为
轴所成的锐角为![]() ,直线
,直线![]() 与
与![]() 轴所成的锐角为
轴所成的锐角为![]() ,判断
,判断![]() 与
与![]() 的大小关系并加以证明.
的大小关系并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月,“一带一路”沿线的20国青年评选出了中国“新四大发明”:高铁、支付宝、共享单车和网购.2017年末,“支付宝大行动”用发红包的方法刺激支付宝的使用.某商家统计前5名顾客扫描红包所得金额分别为5.5元,2.1元,3.3元,5.9元,4.7元,商家从这5名顾客中随机抽取3人赠送台历.
(1)求获得台历是三人中至少有一人的红包超过5元的概率;
(2)统计一周内每天使用支付宝付款的人数![]() 与商家每天的净利润
与商家每天的净利润![]() 元,得到7组数据,如表所示,并作出了散点图.
元,得到7组数据,如表所示,并作出了散点图.

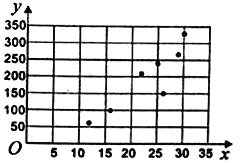
(i)直接根据散点图判断,![]() 与
与![]() 哪一个适合作为每天的净利润的回归方程类型.(
哪一个适合作为每天的净利润的回归方程类型.(![]() 的值取整数)
的值取整数)
(ii)根据(i)的判断,建立![]() 关于
关于![]() 的回归方程,并估计使用支付宝付款的人数增加到35时,商家当天的净利润.
的回归方程,并估计使用支付宝付款的人数增加到35时,商家当天的净利润.
参考数据:
|
|
|
|
22.86 | 194.29 | 268.86 | 3484.29 |
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为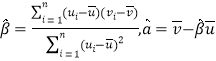 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com