
【题目】若圆的一条直径的两个端点分别是(﹣1,3)和(5,﹣5),则此圆的方程是( )
A.x2+y2+4x+2y﹣20=0
B.x2+y2﹣4x﹣2y﹣20=0
C.x2+y2﹣4x+2y+20=0
D.x2+y2﹣4x+2y﹣20=0
【答案】D
【解析】解:∵(﹣1,3)和(5,﹣5)为一条直径的两个端点,
∴两点的中点(2,﹣1)为圆的圆心,
又两点间的距离d= ![]() =10,
=10,
∴圆的半径为5,
则所求圆的方程为(x﹣2)2+(y+1)2=25,即x2+y2﹣4x+y﹣20=0.
故选D
【考点精析】根据题目的已知条件,利用圆的一般方程的相关知识可以得到问题的答案,需要掌握圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显.


科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,过椭圆M: ![]() (a>b>0)右焦点的直线x+y﹣
(a>b>0)右焦点的直线x+y﹣ ![]() =0交M于A,B两点,P为AB的中点,且OP的斜率为
=0交M于A,B两点,P为AB的中点,且OP的斜率为 ![]() . (Ⅰ)求M的方程
. (Ⅰ)求M的方程
(Ⅱ)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线x2+y=8与x轴交于A,B两点,动点P与A,B连线的斜率之积为 ![]() .
.
(1)求动点P的轨迹C的方程.
(2)MN是动点P轨迹C的一条弦,且直线OM,ON的斜率之积为 ![]() .求
.求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}是首项为0的递增数列,fn(x)=|sin ![]() (x﹣an)|,x∈[an , an+1],n∈N* , 满足:对于任意的b∈[0,1),fn(x)=b总有两个不同的根,则{an}的通项公式为
(x﹣an)|,x∈[an , an+1],n∈N* , 满足:对于任意的b∈[0,1),fn(x)=b总有两个不同的根,则{an}的通项公式为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300)分组的频率分布直方图如图. 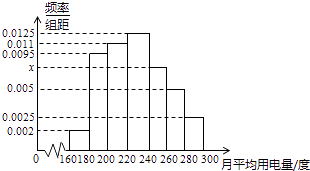
(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,[220,240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣ ![]() x+
x+ ![]() ,若数列{bn}满足:b1=1,bn+1=2f(bn)(n∈N*).若对n∈N* , 都M∈Z,使得
,若数列{bn}满足:b1=1,bn+1=2f(bn)(n∈N*).若对n∈N* , 都M∈Z,使得 ![]() <M恒成立,则整数M的最小值是( )
<M恒成立,则整数M的最小值是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某毕业生参加人才招聘会,分别向甲、乙、丙三个公司投递了个人简历,假定该毕业生得到甲公司面试的概率为 ![]() ,得到乙公司和丙公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记ξ为该毕业生得到面试的公司个数,若P(ξ=0)=
,得到乙公司和丙公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记ξ为该毕业生得到面试的公司个数,若P(ξ=0)= ![]()
(Ⅰ)求p的值:
(Ⅱ)求随机变量ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1(﹣1,0),F2(1,0)是椭圆C1与双曲线C2共同的焦点,椭圆的一个短轴端点为B,直线F1B与双曲线的一条渐近线平行,椭圆C1与双曲线C2的离心率分别为e1 , e2 , 则e1+e2取值范围为( )
A.[2,+∞)
B.[4,+∞)
C.(4,+∞)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD与BDEF均为菱形,设AC与BD相交于点O,若∠DAB=∠DBF=60°,且FA=FC. 
(1)求证:FC∥平面EAD;
(2)求直线AF与平面BCF所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com