【答案】
分析:(I)求导函数f'(x)=3x
2-3a,利用函数f(x)=x
3-3ax+b在x=1处有极小值2,可得
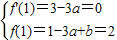
,从而可求函数f(x)的解析式;
(Ⅱ)
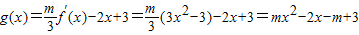
,再进行分类讨论:当m=0时,g(x)=-2x+3,g(x)在[0,2]上有一个零点;当m≠0时,①若方程g(x)=0在[0,2]上有2个相等实根,即函数g(x)在[0,2]上有一个零点;②若g(x)有2个零点,1个在[0,2]内,另1个在[0,2]外,从而可求m的取值范围.
解答:解:(I)f'(x)=3x
2-3a…(1分)
依题意有
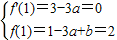
,…(3分)
解得
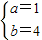
,…(4分)
此时f'(x)=3x
2-3=3(x-1)(x+1),
x∈(-1,1),f'(x)<0,x∈(1,+∞),f'(x)>0,满足f(x)在x=1处取极小值
∴f(x)=x
3-3x+4…(5分)
(Ⅱ)f'(x)=3x
2-3
∴
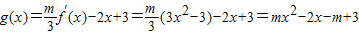
…(6分)
当m=0时,g(x)=-2x+3,
∴g(x)在[0,2]上有一个零点
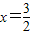
(符合),…(8分)
当m≠0时,
①若方程g(x)=0在[0,2]上有2个相等实根,即函数g(x)在[0,2]上有一个零点.
则
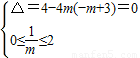
,得
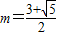
…(10分)
②若g(x)有2个零点,1个在[0,2]内,另1个在[0,2]外,
则g(0)g(2)≤0,即(-m+3)(3m-1)≤0,解得
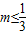
,或m≥3…(12分)
经检验m=3有2个零点,不满足题意.
综上:m的取值范围是
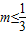
,或
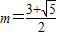
,或m>3…(14分)
点评:本题以函数的性质为载体,考查函数的解析式,考查导数知识的运用,考查函数的零点,考查分类讨论的数学思想,综合性强.

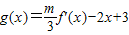 在[0,2]只有一个零点,求m的取值范围.
在[0,2]只有一个零点,求m的取值范围.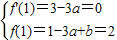 ,从而可求函数f(x)的解析式;
,从而可求函数f(x)的解析式;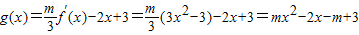 ,再进行分类讨论:当m=0时,g(x)=-2x+3,g(x)在[0,2]上有一个零点;当m≠0时,①若方程g(x)=0在[0,2]上有2个相等实根,即函数g(x)在[0,2]上有一个零点;②若g(x)有2个零点,1个在[0,2]内,另1个在[0,2]外,从而可求m的取值范围.
,再进行分类讨论:当m=0时,g(x)=-2x+3,g(x)在[0,2]上有一个零点;当m≠0时,①若方程g(x)=0在[0,2]上有2个相等实根,即函数g(x)在[0,2]上有一个零点;②若g(x)有2个零点,1个在[0,2]内,另1个在[0,2]外,从而可求m的取值范围.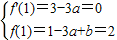 ,…(3分)
,…(3分)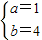 ,…(4分)
,…(4分)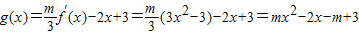 …(6分)
…(6分)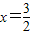 (符合),…(8分)
(符合),…(8分)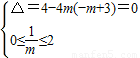 ,得
,得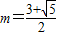 …(10分)
…(10分)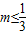 ,或m≥3…(12分)
,或m≥3…(12分)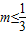 ,或
,或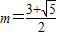 ,或m>3…(14分)
,或m>3…(14分)

 阅读快车系列答案
阅读快车系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<