
����Ŀ��Ϊ��ף����ڣ�ij��ѧ��ί��֯������������������л���֪ʶ�������Ӳμӿ��Ե�ѧ���г��60��������ɼ�(�ɼ���Ϊ����)�ֳ�[40��50)��[50��60)������[90��100)���飬��������ͼ��ʾ�IJ���Ƶ�ʷֲ�ֱ��ͼ���۲�ͼ�Σ��ش��������⣺
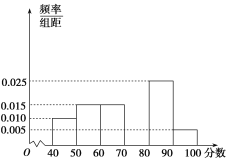
(1)��������Ƶ�ʣ�����ȫ���Ƶ�ʷֲ�ֱ��ͼ��
(2)������ο��Եļ�����(60�ּ�����Ϊ����)��ƽ���֣�
���𰸡�(1)0.3��ͼ��������(2) ��������75%��ƽ����Ϊ71�֣�
��������
(1)���ø����Ƶ�ʺ͵���1����
(2)�����ʾ���[60,100]֮���Ƶ��֮�ͣ�ƽ�������������е�ֵ��Ƶ�ʻ��������.
�⣺(1)��Ϊ�����Ƶ�ʺ͵���1��
���Ե������Ƶ��Ϊ![]() .
.
��ȫ��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��

(2)������ɵõ������ġ��塢�����Ƶ��֮��Ϊ(0.015��0.030��0.025��0.005)��10��0.75��
��ɹ�����ο��Եļ�������75%.
��Ϊ��ȡѧ����ƽ����ԼΪ45��0.1��55��0.156��65��0.15��75��0.3��85��0.25��95��0.05��71(��)�����Կɹ�����ο��Ե�ƽ����Ϊ71�֣�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
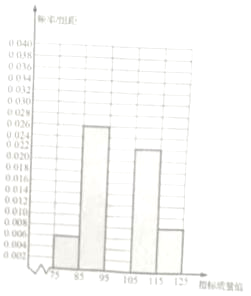
����Ŀ����ij��ҵ������ij�ֲ�Ʒ�г�ȡ100����������Щ��Ʒ��һ������ָ��ֵ���ɲ������õ�����Ƶ�ʷֲ�ֱ��ͼ
��1����ȫ�����Ƶ�ʷֲ�ֱ��ͼ������Ӱ��ʾ����
��2��ͳ�Ʒ����У�ͬһ�����ݳ��ø���������м�ֵ��Ϊ�������ݴ˹������ֲ�Ʒ����ָ��ֵ������̬�ֲ�Z���̣���2�������Ц̽���Ϊ����ƽ��ֵ![]() ����2����Ϊ��������s2��������ȡ�м�ֵ����
����2����Ϊ��������s2��������ȡ�м�ֵ����
�����ø���̬�ֲ�����Ӹó������IJ�Ʒ����ȡһ�����ò�ƷΪ�ϸ�Ʒ�ĸ��ʣ�
�ڸ���ҵÿ���������ֲ�Ʒ10���������һ���ϸ�Ʒ����10Ԫ������һ�����ϸ�Ʒ����20Ԫ�������ҵ���������Ƕ��٣�
�ο����ݣ�![]() ��5.1����Z��N���̣���2������P���̩��ң���+�ң���0.6826��P���̩�2�ң���+2�ң���0.9544��
��5.1����Z��N���̣���2������P���̩��ң���+�ң���0.6826��P���̩�2�ң���+2�ң���0.9544��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ij��ѧ�Ӽ���������ʦ���̰༶��ѧ���������ȡ100�ˣ�ÿ�˷ֱ��������ʦ�������֣����־�Ϊ100�֣������������ݣ���������10Ϊ���ֳ�6�飺![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
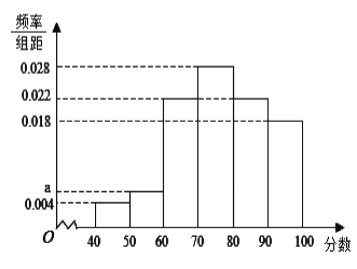
��![]() .�õ���ʦ��Ƶ�ʷֲ�ֱ��ͼ�����ҽ�ʦ��Ƶ���ֲ�����
.�õ���ʦ��Ƶ�ʷֲ�ֱ��ͼ�����ҽ�ʦ��Ƶ���ֲ�����
�ҽ�ʦ����Ƶ���ֲ��� | |
�������� | Ƶ�� |
| 3 |
| 3 |
| 15 |
| 19 |
| 35 |
| 25 |
��1���ڳ�����100���У���Լ�ʦ�����ֵ���70�ֵ�������
��2���Ӷ��ҽ�ʦ��������![]() ��Χ�ڵ��������ѡ��2�ˣ���2�����־���
��Χ�ڵ��������ѡ��2�ˣ���2�����־���![]() ��Χ�ڵĸ��ʣ�
��Χ�ڵĸ��ʣ�
��3�������У��ѧ������ʦ���ֵ���λ���Ƿ����80����Ϊ����һ����ʦ�Ƿ����Ϊ����ȸ�У�����ʦ�ı�����ס���������ʦ����һ������Ϊ��ȸ�У�����ʦ������ȷ��0.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʮ�Ŵ�����������Ӯ��ƶ����ս����������ƶ��ij�����λΪ���������ƶ��������ƶ����ַ�ƶͬ�������ϣ�����ƶ������ֲ��ȣ������û��������̽������ۣ�Ϊ������������ִӸô������������ժ��100����Ƚ��в��أ�����������λ�ˣ��ֲ��������200��500�ڣ���ͳ�Ƶ�������������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.

��1�����ֲ�����ķ�����������![]() ��
��![]() ������������ȡ5�����ٴ���5������������ȡ2��������2���������������һ����С��400�˵ĸ��ʣ�
������������ȡ5�����ٴ���5������������ȡ2��������2���������������һ����С��400�˵ĸ��ʣ�
��2���Ը������ݵ��м���ֵ�����������ݵ�ƽ��ֵ����Ƶ�ʴ�����ʣ���֪�ô�������ֲ���ϴ�Լ����100000����ȴ����ۣ�ij������������չ�������
A.������Ⱦ���7Ԫ/ǧ���չ���
B.����350�˵������2Ԫ/���չ����������3Ԫ/���չ�.
����ͨ������Ϊ�ô�ѡ������Ϻõķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��
��![]() ��ֱ��
��ֱ��![]() ������
������![]() .
.
��1����![]() ��Բ
��Բ![]() ���У���
���У���![]() �ķ��̣�
�ķ��̣�
��2����![]() ��Բ
��Բ![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬��������
���㣬��������![]() ��������ֵ�������ʱ
��������ֵ�������ʱ![]() ��ֱ�߷���.
��ֱ�߷���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й����ʴ����ݲ�ҵ�������ڼ䣬�мס��ҡ�������4���ο��������ݵĻƹ����ٲ�����ɽ������������������βιۣ����е�ÿ����ֻȥһ�����㣬ÿ����������Ҫȥһ���ˣ����οͼ�ȥ��ɽ�ĸ���Ϊ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н��ܲ���Ϊ�������½���ٰ콻֪ͨʶ�ʴ�������Ը���15��65�����Ⱥ�������ش�����ͳ�ƽ����ͼ����ʾ��

��� | ���� | �ش���ȷ������ | �ش���ȷ������ռ����ĸ��� |
��1�� | [15,25) | 5 | 0.5 |
��2�� | [25,35) |
| 0.9 |
��3�� | [35,45) | 27 |
|
��4�� | [45,55) |
| 0.36 |
��5�� | [55,65) | 3 |
|
��1���ֱ����![]() ��ֵ��
��ֵ��
��2���ӵ�2��3��4��ش���ȷ�������÷ֲ����������ȡ6�ˣ����2��3��4��ÿ��Ӧ����ȡ������?
��3���ڣ�2����ǰ���£�����������ȡ��6���������ȡ2�˰䷢���˽���������ȡ�����е�2��������1�˻�����˽��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����
����![]() ��
��![]() ������
������![]() ��
��![]() ��ȡ�ü�ֵ��
��ȡ�ü�ֵ��
![]() 1
1![]() ��
��![]() ʱ����
ʱ����![]() �ĵ������䣻
�ĵ������䣻
![]() 2
2![]() ��
��![]() ��
��![]() �ϵ����ֵΪ1����
�ϵ����ֵΪ1����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com