
【题目】已知定义域为R的函数![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)解关于t的不等式f(t2-2t)+f(2t2-1)<0.
【答案】(1)2;(2)![]()
【解析】
(1)根据奇函数性质的f(0)=0解得b,再根据f(1)=-f(-1)解得a,(2)先判断函数f(x)单调性,再根据奇函数性质以及单调性化简不等式为t2-2t>-2t2+1,解一元二次不等式得结果.
(1)因为f(x)是定义在R上的奇函数,
所以f(0)=0,
即![]() =0,解得b=1,
=0,解得b=1,
所以f(x)=![]() .
.
又由f(1)=-f(-1)知![]() =-
=-![]() ,解得a=2.
,解得a=2.
(2)由(1)知f(x)=![]() =-
=-![]() +
+![]() .
.
由上式易知f(x)在(-∞,+∞)上为减函数(此处可用定义或导数法证明函数f(x)在R上是减函数).
又因为f(x)是奇函数,所以不等式f(t2-2t)+f(2t2-1)<0等价于f(t2-2t)<-f(2t2-1)=f(-2t2+1).
因为f(x)是减函数,由上式推得t2-2t>-2t2+1,
即3t2-2t-1>0,解不等式可得t>1或t<-![]() ,
,
故原不等式的解集为![]() .
.


科目:高中数学 来源: 题型:
【题目】小明一家订阅的晚报会在下午5:30~6:30之间的任何一个时间随机地被送到,小明一家人在下午6:00~7:00之间的任何一个时间随机地开始晚餐.
(1)你认为晚报在晚餐开始之前被送到和晚餐开始之后被送到哪一种可能性更大?
(2)晚报在晚餐开始之前被送到的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 且S2=11,S5=50,则过点P(n,an)和Q(n+2,an+2)(n∈N*)的直线的一个方向向量的坐标可以是( )
A.(﹣1,﹣3)
B.(1,﹣3)
C.(1,1)
D.(1,﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形![]() 的对角线
的对角线![]() 与
与![]() 相交于
相交于![]() 点,将
点,将![]() 沿对角线折起,使得平面
沿对角线折起,使得平面![]() 平面
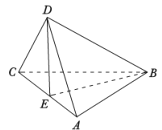
平面![]() (如图),则下列命题中正确的是( )
(如图),则下列命题中正确的是( )
A. 直线![]() 直线
直线![]() ,且直线
,且直线![]() 直线
直线![]()
B. 直线![]() 平面
平面![]() ,且直线
,且直线![]() 平面
平面![]()
C. 平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
D. 平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={(x,y)|y=f(x)},若对于任意实数对(x1,y1)∈M,存在(x2,y2)∈M,使x1x2+y1y2=0成立,则称集合M具有∟性,给出下列四个集合:
①M={(x,y)|y=x3﹣2x2+3}; ②M={(x,y)|y=log2(2﹣x)};
③M={(x,y)|y=2﹣2x}; ④M={(x,y)|y=1﹣sinx};
其中具有∟性的集合的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,直线y=
,直线y= ![]() x为曲线y=f(x)的切线(e为自然对数的底数).
x为曲线y=f(x)的切线(e为自然对数的底数).
(1)求实数a的值;
(2)用min{m,n}表示m,n中的最小值,设函数g(x)=min{f(x),x﹣ ![]() }(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
}(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com