
【题目】设![]() ,
,![]() 分别是椭圆C:
分别是椭圆C:![]() 的左、右焦点,过
的左、右焦点,过![]() 且斜率不为零的动直线l与椭圆C交于A,B两点.
且斜率不为零的动直线l与椭圆C交于A,B两点.
![]() Ⅰ
Ⅰ![]() 求
求![]() 的周长;
的周长;
![]() Ⅱ
Ⅱ![]() 若存在直线l,使得直线
若存在直线l,使得直线![]() ,AB,
,AB,![]() 与直线
与直线![]() 分别交于P,Q,R三个不同的点,且满足P,Q,R到x轴的距离依次成等比数列,求该直线l的方程.
分别交于P,Q,R三个不同的点,且满足P,Q,R到x轴的距离依次成等比数列,求该直线l的方程.

科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别是离心率为
分别是离心率为![]() 的椭圆
的椭圆![]() :
:![]() 的左、右焦点,点
的左、右焦点,点![]() 是椭圆
是椭圆![]() 上异于其左、右顶点的任意一点,过右焦点
上异于其左、右顶点的任意一点,过右焦点![]() 作
作![]() 的外角平分线
的外角平分线![]() 的垂线
的垂线![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() (
(![]() 为坐标原点).
为坐标原点).
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 在圆
在圆![]() 上,且在第一象限,过
上,且在第一象限,过![]() 作圆
作圆![]() 的切线交椭圆于
的切线交椭圆于![]() 、
、![]() 两点,问:
两点,问:![]() 的周长是否为定值?如果是,求出该定值;如果不是,说明理由.
的周长是否为定值?如果是,求出该定值;如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() .以坐标原点为极点,以
.以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() .若点
.若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() ,
,![]() 两点间的距离
两点间的距离![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ( x R ,且 e 为自然对数的底数).
( x R ,且 e 为自然对数的底数).
⑴ 判断函数 f x 的单调性与奇偶性;
⑵是否存在实数 t ,使不等式![]() 对一切的 x R 都成立?若存在,求出 t 的值,若 不存在说明理由.
对一切的 x R 都成立?若存在,求出 t 的值,若 不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为![]() (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为![]() (m2).
(m2).

(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=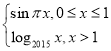 ,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围是( )
A. (1,2015)B. (1,2016)
C. [2,2 016]D. (2,2016)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市经营一批产品,在市场销售中发现此产品在30天内的日销售量P(件)与日期![]() )之间满足
)之间满足![]() ,已知第5日的销售量为55件,第10日的销售量为50件。
,已知第5日的销售量为55件,第10日的销售量为50件。
(1)求第20日的销售量; (2)若销售单价Q(元/件)与![]() 的关系式为
的关系式为![]() ,求日销售额
,求日销售额![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,长轴端点与短轴端点间的距离为
,长轴端点与短轴端点间的距离为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)设过点![]()
![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() 为直角三角形,求直线
为直角三角形,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com