
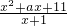 (a∈R),若对于任意的X∈N*,f(x)≥3恒成立,则a的取值范围是________.
(a∈R),若对于任意的X∈N*,f(x)≥3恒成立,则a的取值范围是________.
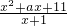 ≥3转化为a≥-
≥3转化为a≥- -x+3,再令g(x)=-
-x+3,再令g(x)=- -x+3(x∈N*),利用其单调性可求得g(x)max,从而可得答案.
-x+3(x∈N*),利用其单调性可求得g(x)max,从而可得答案.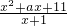 ≥3恒成立?x2+ax+11≥3x+3恒成立,
≥3恒成立?x2+ax+11≥3x+3恒成立, -x+3恒成立,
-x+3恒成立, -x+3(x∈N*),再令h(x)=x+
-x+3(x∈N*),再令h(x)=x+ (x∈N*),
(x∈N*), 在(0,2
在(0,2 ]上单调递减,在[2
]上单调递减,在[2 ,+∞)上单调递增,而x∈N*,
,+∞)上单调递增,而x∈N*, 较近的整数值时达到最小,而距离2
较近的整数值时达到最小,而距离2 较近的整数为2和3,
较近的整数为2和3, ,h(2)>h(3),
,h(2)>h(3), .又g(x)=-
.又g(x)=- -x+3=-h(x)+3,
-x+3=-h(x)+3, +3=-
+3=- .
. .
. -x+3是关键,考查转化思想,构造函数的思想,考查函数的单调性的应用,综合性强,思维度深,属于难题.
-x+3是关键,考查转化思想,构造函数的思想,考查函数的单调性的应用,综合性强,思维度深,属于难题. 

科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| m |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com