
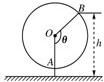
 如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离是h.
如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离是h.| π |
| 30 |
| π |
| 30 |
| π |
| 30 |
 解:(1)以圆心O为原点,建立如图所示的平面直角坐标系,
解:(1)以圆心O为原点,建立如图所示的平面直角坐标系,| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 30 |
| π |
| 30 |
| π |
| 30 |
| π |
| 2 |
| π |
| 30 |
| π |
| 2 |
| π |
| 30 |
| π |
| 2 |
| π |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2011年《金版新学案》高三数学(文科)一轮复习测评卷:章末质量检测04(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:新课标高三数学三角函数专项训练(河北) 题型:解答题
如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离是h.
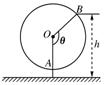
(1)求h与θ间的函数关系式;
(2)设从OA开始转动,经过t秒后到达OB,求h与t之间的函数关系式,并求缆车到达最高点时用的最少时间是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com