解:(1)设双曲线E的方程为
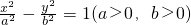
,则B(-c,0),D(a,0),C(c,0).
由BD=3DC,得c+a=3(c-a),即c=2a.
∴
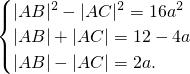
,解之得a=1,∴
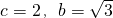
.
∴双曲线E的方程为

.
(2)设在x轴上存在定点G(t,0),使
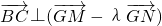
.
设直线l的方程为x-m=ky,M(x
1,y
1),N(x
2,y
2).
由
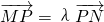
,得y
1+λy
2=0.
即λ=-

①
∵

=(4,0),
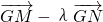
=(x
1-t-λx
2+λt,y
1-λy
2)
∴x
1-t-λx
2+λt=0
∴x
1-t=λ(x
2-t)
即ky
1+m-t=λ(ky
2+m-t)②
①代入②得2ky
1y
2+(m-t)(y
1+y
2)=0③
把x=m+ky代入双曲线,消去x可得(3k
2-1)y
2+6kmy+3(m
2-1)=0
∴y
1+y
2=
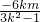
,y
1y
2=
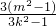
代入③可得
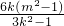
-
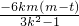
=0
化简可得kmt=k
当t=

时,上式恒成立
因此,在x轴上存在定点G(

,0),使
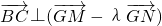
.
分析:(1)设双曲线E的方程,利用BD=3DC,△ABC的周长为12,建立方程,即可求得双曲线的方程;
(2)对于存在性问题,可先假设存在,即假设在x轴上存在定点G(t,0),再利用根与系数的关系,求出t的值,若出现矛盾,则说明假设不成立,即不存在;否则存在.
点评:本题主要考查直线与圆锥曲线的综合问题、向量的运算、双曲线方程等基础知识,考查运算求解能力、化归与转化思想.属于中档题.

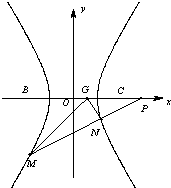 如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.
如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.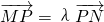 ,问在x轴上是否存在定点G,使
,问在x轴上是否存在定点G,使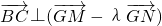 ?若存在,求出所有这样定点G的坐标;若不存在,请说明理由.
?若存在,求出所有这样定点G的坐标;若不存在,请说明理由.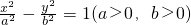 ,则B(-c,0),D(a,0),C(c,0).
,则B(-c,0),D(a,0),C(c,0).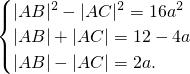 ,解之得a=1,∴
,解之得a=1,∴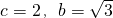 .
. .
.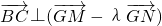 .
.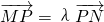 ,得y1+λy2=0.
,得y1+λy2=0. ①
① =(4,0),
=(4,0),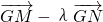 =(x1-t-λx2+λt,y1-λy2)
=(x1-t-λx2+λt,y1-λy2)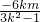 ,y1y2=
,y1y2=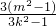
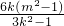 -
-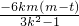 =0
=0 时,上式恒成立
时,上式恒成立 ,0),使
,0),使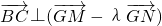 .
.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案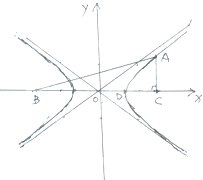 如图,直角坐标系xoy中,有Rt△ABC,∠C=90°,D在边BC上,BD=3DC,双曲线E以B、C为焦点,且经过A、D两点.
如图,直角坐标系xoy中,有Rt△ABC,∠C=90°,D在边BC上,BD=3DC,双曲线E以B、C为焦点,且经过A、D两点.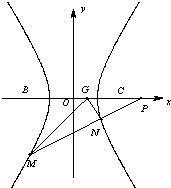 如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点.
如图,直角坐标系xOy中,一直角三角形ABC,∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点. (2012•芜湖二模)如图,直角坐标系XOY中,点F在x轴正半轴上,△OFG的面积为S.且
(2012•芜湖二模)如图,直角坐标系XOY中,点F在x轴正半轴上,△OFG的面积为S.且 如图在直角坐标系xoy中,圆O与x轴交于A、B两点,且|AB|=4,定直线l垂直于x轴正半轴,且到圆心O的距离为4,点P是圆O上异于A、B的任意一点,直线PA、PB分别交l于点M、N.
如图在直角坐标系xoy中,圆O与x轴交于A、B两点,且|AB|=4,定直线l垂直于x轴正半轴,且到圆心O的距离为4,点P是圆O上异于A、B的任意一点,直线PA、PB分别交l于点M、N.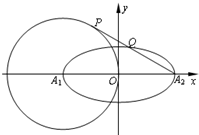 如图平面直角坐标系xOy中,椭圆
如图平面直角坐标系xOy中,椭圆