
【题目】某水泥厂销售工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示:
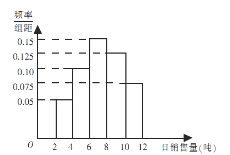
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求未来3天内,连续2天日销售量不低于8吨,另一天日销售量低于8吨的概率;
(2)用![]() 表示未来3天内日销售量不低于8吨的天数,求随机变量
表示未来3天内日销售量不低于8吨的天数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)![]() ;(2)
;(2) ![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
![]() .
.
【解析】
试题分析:(1) 在频率直方图中,大于![]() 吨的两个矩形的面积即为日销售量不低于
吨的两个矩形的面积即为日销售量不低于![]() 吨的频率,未来三天内连续
吨的频率,未来三天内连续![]() 天日销售不低于
天日销售不低于![]() 吨,另一天日销量低于
吨,另一天日销量低于![]() 吨包含两个互斥事件,即第一、二天高于
吨包含两个互斥事件,即第一、二天高于![]() 吨第三天低于
吨第三天低于![]() 吨与第一天低于
吨与第一天低于![]() 吨而第二、三天高于
吨而第二、三天高于![]() 吨,分别计算其概率相加即可;(2)
吨,分别计算其概率相加即可;(2) ![]() 的可能取值为
的可能取值为![]() ,且
,且![]() ~
~![]() ,由二项分布公式计算其相应的概率及期望即可.
,由二项分布公式计算其相应的概率及期望即可.
试题解析: (Ⅰ)由频率分布直方图可知,日销售量不低于![]() 吨的频率为:
吨的频率为:
![]() ,……………………(1分)
,……………………(1分)
记未来![]() 天内,第
天内,第![]() 天日销售量不低于
天日销售量不低于![]() 吨为事件
吨为事件![]() ,则
,则![]() ,………………(2分)
,………………(2分)
未来![]() 天内,连续
天内,连续![]() 天日销售不低于
天日销售不低于![]() 吨,另一天日销量低于
吨,另一天日销量低于![]() 吨包含两个互斥事件
吨包含两个互斥事件![]() 和
和![]() ,………………(3分)
,………………(3分)
则:![]() ………………(4分)
………………(4分)
![]() .………………(6分)
.………………(6分)
(Ⅱ)![]() 的可能取值为
的可能取值为![]() ,且
,且![]() ~
~![]()
![]() ,………………(7分)
,………………(7分)
![]() ,………………(8分)
,………………(8分)
![]() ,………………(9分)
,………………(9分)
![]() ,………………(10分)
,………………(10分)
所以![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
…………(11分)
![]() .………………(12分)
.………………(12分)


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】某区工商局、消费者协会在![]() 月
月![]() 号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取
号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的群众中随机抽取![]() 名群众,按他们的年龄分组:第
名群众,按他们的年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
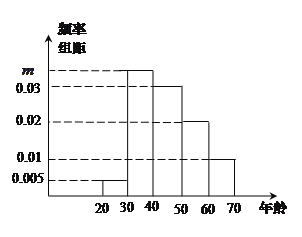
(Ⅰ)若电视台记者要从抽取的群众中选![]() 人进行采访,求被采访人恰好在第
人进行采访,求被采访人恰好在第![]() 组或第
组或第![]() 组的概率;
组的概率;
(Ⅱ)已知第![]() 组群众中男性有
组群众中男性有![]() 人,组织方要从第
人,组织方要从第![]() 组中随机抽取
组中随机抽取![]() 名群众组成维权志愿者服务队,求至少有两名女性的概率.
名群众组成维权志愿者服务队,求至少有两名女性的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前3项和为6,前8项和为-4.
(1)求数列{an}的通项公式;
(2)设bn=(4-an)qn-1 (q≠0,n∈N*),求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,两焦点
,两焦点![]() ,点
,点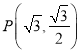 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
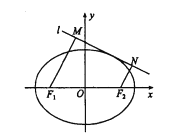
(2)如图,动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,点
有且仅有一个公共点,点![]() 、
、![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() .求四边形
.求四边形![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),当
为参数),当![]() 时,曲线
时,曲线![]() 上对应的点为
上对应的点为![]() .以原点
.以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)设曲线![]() 与
与![]() 的公共点为
的公共点为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以平面直角坐标系的原点
为参数).以平面直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 和
和![]() 公共弦的长度.
公共弦的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图①,正三角形![]() 的边长为4,
的边长为4,![]() 是
是![]() 边上的高,
边上的高,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 边的中点,现将△
边的中点,现将△![]() 沿
沿![]() 翻折成直二面角
翻折成直二面角![]() ,如图②.
,如图②.
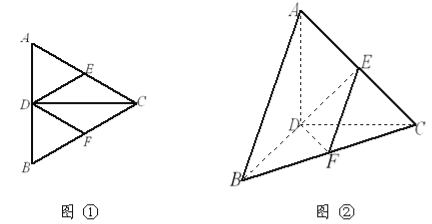
(1)判断直线![]() 与平面
与平面![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com