
分析 (1)由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,代入曲线C的极坐标方程,即可得到所求直角坐标方程;运用直线的参数方程:$\left\{\begin{array}{l}{x={x}_{0}+tcosα}\\{y={y}_{0}+tsinα}\end{array}\right.$(t为参数),可得所求;
(2)将直线的参数方程,代入曲线C的直角坐标方程,化简整理,运用韦达定理,即可得到所求和.
解答 解:(1)由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,
ρ=2cosθ得ρ2=2ρcosθ,
即为x2+y2=2x即(x-1)2+y2=1;
又因为直线l过点M(5,$\sqrt{3}$),且倾斜角为$\frac{π}{6}$,
可得直线l的参数方程为$\left\{\begin{array}{l}{x=5+tcos\frac{π}{6}}\\{y=\sqrt{3}+tsin\frac{π}{6}}\end{array}\right.$,
即为$\left\{\begin{array}{l}{x=5+\frac{\sqrt{3}}{2}t}\\{y=\sqrt{3}+\frac{1}{2}t}\end{array}\right.$(t为参数);
(2)设A,B两点对应的参数分别为t1,t2,
将直线l的参数方程代入圆的直角坐标方程(x-1)2+y2=1,
得(4+$\frac{\sqrt{3}}{2}$t)2+($\sqrt{3}$+$\frac{1}{2}$t)2=1,
化简得t2+5$\sqrt{3}$t+18=0,
即有t1+t2=-5$\sqrt{3}$,t1t2=18,
可得|MA|+|MB|=|t1|+|t2|=|t1+t2|=5$\sqrt{3}$.
点评 本题考查极坐标方程和直角坐标方程的互化,以及直线的参数方程的求法,同时考查直线参数方程的运用,考查运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
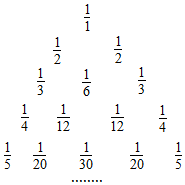 如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数之和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,则第n(n≥4)行倒数第四个数(从右往左数)为$\frac{1}{{n•C_{n-1}^3}}$或$\frac{6}{n(n-1)(n-2)(n-3)}$.
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为$\frac{1}{n}$(n≥2),每个数是它下一行左右相邻两数之和,如$\frac{1}{1}$=$\frac{1}{2}$+$\frac{1}{2}$,$\frac{1}{2}$=$\frac{1}{3}$+$\frac{1}{6}$,$\frac{1}{3}$=$\frac{1}{4}$+$\frac{1}{12}$,…,则第n(n≥4)行倒数第四个数(从右往左数)为$\frac{1}{{n•C_{n-1}^3}}$或$\frac{6}{n(n-1)(n-2)(n-3)}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
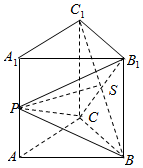 已知直三棱柱ABC-A1B1C1的各棱长均为a,点P是侧棱AA1的中点,BC1∩B1C=S
已知直三棱柱ABC-A1B1C1的各棱长均为a,点P是侧棱AA1的中点,BC1∩B1C=S查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点C是圆O直径BE的延长线上一点,AC是圆O的切线,A为切点,∠ACB的平分线CD分别与AB、AE交于D、F.
如图,点C是圆O直径BE的延长线上一点,AC是圆O的切线,A为切点,∠ACB的平分线CD分别与AB、AE交于D、F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
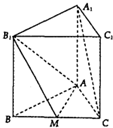 如图,三棱柱ABC-A1B1C1的所有棱长都为1,且侧棱与底面垂直,M是BC的中点.
如图,三棱柱ABC-A1B1C1的所有棱长都为1,且侧棱与底面垂直,M是BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com