
【题目】四棱锥![]() 与直四棱柱
与直四棱柱![]() 组合而成的几何体中,四边形
组合而成的几何体中,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)动点![]() 在线段
在线段![]() 上(包括端点),若二面角
上(包括端点),若二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长度.
的长度.
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
(1)证明:BE⊥DC;
(2)求直线BE与平面PBD所成角的正弦值;
(3)若F为棱PC上一点,满足BF⊥AC,求二面角F-AB-P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,椭圆
,椭圆![]() 上短轴的一个端点与两个焦点构成的三角形的面积为
上短轴的一个端点与两个焦点构成的三角形的面积为![]() ;
;
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在第二象限),
在第二象限),![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点,若
两侧的动点,若![]() ,求证:直线
,求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据我市房地产数据显示,今年我市前5个月新建住宅销售均价逐月上升,为抑制房价过快上涨,政府从6月份开始推出限价房等宏观调控措施,6月份开始房价得到很好的抑制,房价回落.今年前10个月的房价均价如表:
月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
均价y(万元/平方米) | 0.83 | 0.95 | 1.00 | 1.05 | 1.17 | 1.15 | 1.10 | 1.06 | 0.98 | 0.94 |
地产数据研究发现,从1月份至5月份的各月均价y(万元/平方米)与x之间具有正线性相关关系,从6月份至10月份的各月均价y(万元/平方米)与x之间具有负线性相关关系.
(1)若政府不调控,根据前5个月的数据,求y关于x的回归直线方程,并预测12月份的房地产均价.(精确到0.01)
(2)政府调控后,从6月份至10月份的数据可得到y与x的回归直线方程为:![]() .由此预测政府调控后12月份的房地产均价.说明政府调控的必要性.(精确到0.01)
.由此预测政府调控后12月份的房地产均价.说明政府调控的必要性.(精确到0.01)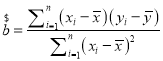 ;
;![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B是抛物线C:y2=4x上两点,线段AB的垂直平分线与x轴有唯一的交点P(x0,0).
(1)求证:x0>2;
(2)若直线AB过抛物线C的焦点F,且|AB|=10,求|PF|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过点F的直线l交抛物线于A,B两点,以线段AB为直径的圆交x轴于M,N两点,设线段AB的中点为Q.若抛物线C上存在一点
的焦点为F,过点F的直线l交抛物线于A,B两点,以线段AB为直径的圆交x轴于M,N两点,设线段AB的中点为Q.若抛物线C上存在一点![]() 到焦点F的距离等于3.则下列说法正确的是( )
到焦点F的距离等于3.则下列说法正确的是( )
A.抛物线的方程是![]() B.抛物线的准线是
B.抛物线的准线是![]()
C.![]() 的最小值是
的最小值是![]() D.线段AB的最小值是6
D.线段AB的最小值是6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com