
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
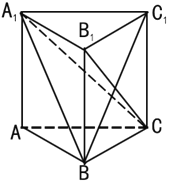
(1)求证:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(3)点![]() 在线段
在线段![]() 上,且
上,且![]() ,点
,点![]() 在线段
在线段![]() 上,若
上,若![]() 平面
平面![]() ,求
,求![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
(1)根据三棱柱![]() 的结构特征,利用线面垂直的判定定理,证得
的结构特征,利用线面垂直的判定定理,证得![]() 平面
平面![]() ,得到
,得到![]() ,再利用线面垂直的判定定理,即可证得
,再利用线面垂直的判定定理,即可证得![]() 平面
平面![]() ;
;
(2)由(1)得到![]() ,建立空间直角坐标系
,建立空间直角坐标系![]() ,求得向量
,求得向量![]() ,利用向量的夹角公式,即可求解.
,利用向量的夹角公式,即可求解.
(3)由![]() ,得
,得![]() ,设
,设![]() ,得
,得![]() ,求得向量
,求得向量![]() 的坐标,结合
的坐标,结合![]() 平面
平面![]() ,利用
,利用![]() ,即可求解.
,即可求解.
(1)在三棱柱![]() 中,由
中,由![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,交线为
,交线为![]() .
.
又因为![]() ,所以
,所以![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]()
又因为![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() .
.
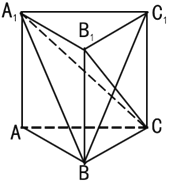
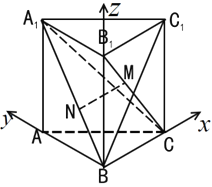
(2)由(1)知![]() 底面
底面![]() ,
,![]() ,如图建立空间直角坐标系
,如图建立空间直角坐标系![]() ,
,
由题意得![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
所以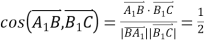 .
.
故异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.

(3)易知平面![]() 的一个法向量
的一个法向量![]() ,
,
由![]() ,得
,得![]() .
.
设![]() ,得
,得![]() ,则
,则![]()
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
即![]() ,解得
,解得![]() ,所以
,所以![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】某环境保护部门对某处的环境状况用“污染指数”来监测,据测定,该处的“污染指数”与附近污染源的强度和距离之比成正比,比例系数为常数![]()
![]() ,现已知相距
,现已知相距![]() 的
的![]() 两家化工厂(污染源)的污染强度分别为1和
两家化工厂(污染源)的污染强度分别为1和![]()
![]() ,它们连线段上任意一点
,它们连线段上任意一点![]() 处的污染指数
处的污染指数![]() 等于两化工厂对该处的污染指数之和,设
等于两化工厂对该处的污染指数之和,设![]() ;
;
(1)试将![]() 表示为
表示为![]() 的函数,指出其定义域;
的函数,指出其定义域;
(2)当![]() 时,
时,![]() 处的“污染指数”最小,试求
处的“污染指数”最小,试求![]() 化工厂的污染强度
化工厂的污染强度![]() 的值;
的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,我们知道当a取不同的值时,得到不同的数列.如当
,我们知道当a取不同的值时,得到不同的数列.如当![]() 时,得到无穷数列:0,
时,得到无穷数列:0,![]() ,
,![]() ,
,![]() ,…,当
,…,当![]() 时,得到有穷数列:
时,得到有穷数列:![]() ,
,![]() ,1.
,1.
(1)当a为何值时,![]() ;
;
(2)设数列![]() 满足
满足![]() ,
,![]() ,求证:a取
,求证:a取![]() 中的任一数,都可以得到一个有穷数列
中的任一数,都可以得到一个有穷数列![]() ;
;
(3)是否存在实数a,使得到的![]() 是无穷数列,且对于任意
是无穷数列,且对于任意![]() ,都有
,都有![]() 成立,若存在,求出a的取值范围;若不存在,请说明理由.
成立,若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每个国家身高正常的标准是不一样的,不同年龄、不同种族、不同地区身高都是有差异的,我们国家会定期进行0~18岁孩子身高体重全国性调查,然后根据这个调查结果制定出相应的各个年龄段的身高标准.一般测量出一个孩子的身高,对照一下身高体重表,如果在平均值标准差以内的就说明你的孩子身高是正常的,否则说明你的孩子可能身高偏矮或偏高了.根据科学研究0~18岁的孩子的身高服从正态分布![]() .在某城市随机抽取100名18岁男大学生得到其身高(
.在某城市随机抽取100名18岁男大学生得到其身高(![]() )的数据.
)的数据.
(1)记![]() 表示随机抽取的100名18岁男大学生身高的数据在
表示随机抽取的100名18岁男大学生身高的数据在![]() 之内的人数,求
之内的人数,求![]() 及
及![]() 的数学期望.
的数学期望.
(2)若18岁男大学生身高的数据在![]() 之内,则说明孩子的身高是正常的.
之内,则说明孩子的身高是正常的.
(i)请用统计学的知识分析该市18岁男大学生身高的情况;
(ii)下面是抽取的100名18岁男大学生中20名大学生身高(![]() )的数据:
)的数据:
1.65 | 1.62 | 1.74 | 1.82 | 1.68 | 1.72 | 1.75 | 1.66 | 1.73 | 1.67 |
1.86 | 1.81 | 1.74 | 1.69 | 1.76 | 1.77 | 1.69 | 1.78 | 1.63 | 1.68 |
经计算得![]() ,
, ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个学生的身高,
个学生的身高,![]() .用样本平均数
.用样本平均数![]() 作为
作为![]() 的估计值,用样本标准差
的估计值,用样本标准差![]() 作为
作为![]() 的估计,剔除
的估计,剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() 的值.(精确到0.01)
的值.(精确到0.01)
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国庆黄金周影市火爆依旧,《我和我的祖国》、《中国机长》、《攀登者》票房不断刷新,为了解我校高三2300名学生的观影情况,随机调查了100名在校学生,其中看过《我和我的祖国》或《中国机长》的学生共有80位,看过《中国机长》的学生共有60位,看过《中国机长》且看过《我和我的祖国》的学生共有50位,则该校高三年级看过《我和我的祖国》的学生人数的估计值为( )
A.1150B.1380C.1610D.1860
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,已知![]() ,顶点P在平面ABC上的射影为
,顶点P在平面ABC上的射影为![]() 的外接圆圆心.
的外接圆圆心.
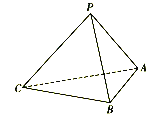
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若点M在棱PA上,![]() ,且二面角P-BC-M的余弦值为
,且二面角P-BC-M的余弦值为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com