
【题目】已知函数![]() ,且
,且![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)当![]() 时,证明:
时,证明: .
.
【答案】(1)当![]() 时,函数
时,函数![]() 有极大值
有极大值![]() ,当
,当![]() 时,函数
时,函数![]() 有极小值
有极小值![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)求极值,可先求得导数![]() ,然后通过解不等式
,然后通过解不等式![]() 确定增区间,解不等式
确定增区间,解不等式![]() 确定减区间,则可得极大值和极小值;(2)要证明此不等式,我们首先研究不等式左边的函数,记
确定减区间,则可得极大值和极小值;(2)要证明此不等式,我们首先研究不等式左边的函数,记![]() ,求出其导数
,求出其导数![]() ,可知
,可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,![]() ,这是
,这是![]() 时最小值,
时最小值,![]() ,这是
,这是![]() 时的最大值,因此要证明题中不等式,可分类,
时的最大值,因此要证明题中不等式,可分类,![]() 和
和![]() 分别证明.
分别证明.
试题解析:(1)依题意,![]() ,
,
故![]() ,
,
令![]() ,则
,则![]() 或
或![]() ; 令
; 令![]() ,则
,则![]() ,
,
故当![]() 时,函数
时,函数![]() 有极大值
有极大值![]() ,当
,当![]() 时,函数
时,函数![]() 有极小值
有极小值![]() .
.
(2) 由(1)知![]() ,令
,令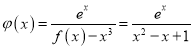 ,
,
则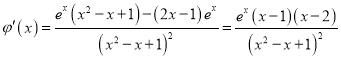 ,
,
可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,令
上单调递减,令![]() .
.
① 当![]() 时,
时,![]() ,所以函数
,所以函数![]() 的图象在
的图象在![]() 图象的上方.
图象的上方.
② 当![]() 时,函数
时,函数![]() 单调递减,所以其最小值为
单调递减,所以其最小值为![]() 最大值为2,而
最大值为2,而![]() ,所以函数
,所以函数![]() 的图象也在
的图象也在![]() 图象的上方.
图象的上方.
综上可知,当![]() 时,
时,


科目:高中数学 来源: 题型:
【题目】给出下列关系:其中具有相关关系的是( )
①考试号与考生考试成绩; ②勤能补拙;
③水稻产量与气候; ④正方形的边长与正方形的面积.
A.①②③B.①③④C.②③D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为![]() 的正项数列
的正项数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)设数列![]() 是公比为
是公比为![]() 的等比数列,
的等比数列,![]() 为数列
为数列![]() 前
前![]() 项的和.若
项的和.若![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() )成等差数列,且
)成等差数列,且![]() ,求正整数
,求正整数![]() 的最小值,以及
的最小值,以及![]() 取最小值时相应数列
取最小值时相应数列![]() ,
,![]() ,
,![]() ,
,![]() 的公差.
的公差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学的父亲决定今年夏天卖西瓜赚钱,根据去年6月份的数据统计连续五天内每天所卖西瓜的个数与温度之间的关系如下表:
温度 | 32 | 33 | 35 | 37 | 38 |
西瓜个数 | 20 | 22 | 24 | 30 | 34 |
(1)求这五天内所卖西瓜个数的平均值和方差;
(2)求变量![]() 之间的线性回归方程,并预测当温度为
之间的线性回归方程,并预测当温度为![]() 时所卖西瓜的个数.
时所卖西瓜的个数.
附: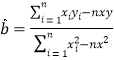 ,
,![]() (精确到
(精确到![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数![]() (
(![]() ,
,![]() )的图像关于直线x=
)的图像关于直线x=![]() 对称,最大值为3,且图像上相邻两个最高点的距离为
对称,最大值为3,且图像上相邻两个最高点的距离为![]() .
.
(1)求![]() 的最小正周期;
的最小正周期;
(2)求函数![]() 的解析式;
的解析式;
(3)若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax-![]() -5ln x,g(x)=x2-mx+4.
-5ln x,g(x)=x2-mx+4.
(1)若x=2是函数f(x)的极值点,求a的值;
(2)当a=2时,若x1∈(0,1),x2∈[1,2],都有f(x1)≥g(x2)成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的不等式ax>1(a>0,a≠1)的解集是{x|x<0},命题q:函数y=lg(ax2-x+a)的定义域为R,如果p∨q为真命题,p∧q为假命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com