
【题目】已知f(x)=m(x-2m)(x+m+3),g(x)=2x-2.若同时满足条件:
①x∈R,f(x)<0或g(x)<0;
②x∈(-∞,-4),f(x)g(x)<0,则m的取值范围是 .
【答案】(-4,-2)
【解析】 g(x)=2x4>0 时 x>2
当x﹤1时,g(x)﹤0,
又∵①x∈R,f(x)<0或g(x)﹤0,
∴f(x)=m(x-2m)(x+m+3)<0在x≥1时恒成立
则由二次函数的性质可知开口只能向下,且二次函数与x轴交点都在(1,0)的左面
则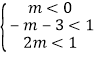
∴-4<m<0,即①成立的范围为-4<m<0
又∵②∈(-∞,-4),f(x) g(x)<0
∴此时g(x)=2x-2<0恒成立
f(x) =m(x-2m)(x+m+3)>0在x∈(-∞,-4)有成立的可能,则只要-4比x1 , x2中的较小的根大即可,
(i)当-1<m<0时,较小的根为-m-3,-m-3<-4不成立
(ii)当m=-1时,两个根同为-2>-4,不成立
(iii)当-4<m<-1时,较小的根为2m,2m<-4,即m<-2成立.
综上可得①②成立时-4<m<-2.
故答案为:(-4,-2)
根据题意当x的取值范围不同时结合指数函数的单调性求解出f(x) >0或f(x) <0的x的解集,进而得到关于m的不等式组解出m的解集即可。


科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=(x+1)ex则对任意的m∈R,函数F(x)=f(f(x))﹣m的零点个数至多有( )
A.3个
B.4个
C.6个
D.9个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美索不达米亚平原是人类文明的发祥地之一.美索不达米亚人善于计算,他们创造了优良的计数系统,其中开平方算法是最具有代表性的.程序框图如图所示,若输入a,n,ξ的值分别为8,2,0.5,(每次运算都精确到小数点后两位)则输出结果为( ) 
A.2.81
B.2.82
C.2.83
D.2.84
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:今有刍童,下广三丈,袤四丈,上袤二丈,无广,高一丈,问:积几何?其意思是说:“今有底面为矩形的屋脊状楔体,下底面宽3丈,长4丈;上棱长2丈,高一丈.问它的体积是多少?”已知一丈为10尺,现将该楔体的三视图给出如右图所示,其中网格纸上小正方形的边长为1,则该楔体的体积为( )
A.5000立方尺
B.5500立方尺
C.6000立方尺
D.6500立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a>1,函数f(x)=(1+x2)ex﹣a.
(1)求f(x)的单调区间;
(2)证明f(x)在(﹣∞,+∞)上仅有一个零点;
(3)若曲线y=f(x)在点P处的切线与x轴平行,且在点M(m,n)处的切线与直线OP平行,(O是坐标原点),证明:m≤ ![]() ﹣1.
﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线 ![]() 平面
平面 ![]() ,垂足为
,垂足为 ![]() ,正四面体(所有棱长都相等的三棱锥)
,正四面体(所有棱长都相等的三棱锥) ![]() 的棱长为2,
的棱长为2, ![]() 在平面
在平面 ![]() 内,
内, ![]() 是直线
是直线 ![]() 上的动点,当
上的动点,当 ![]() 到
到 ![]() 的距离为最大时,正四面体在平面
的距离为最大时,正四面体在平面 ![]() 上的射影面积为 .
上的射影面积为 . 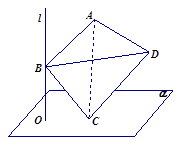
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() ,
, ![]() .过
.过 ![]() 且斜率为
且斜率为 ![]() 的直线
的直线 ![]() 与椭圆
与椭圆 ![]() 相交于点
相交于点 ![]() ,
, ![]() .当
.当 ![]() 时,四边形
时,四边形 ![]() 恰在以
恰在以 ![]() 为直径,面积为
为直径,面积为 ![]() 的圆上.
的圆上.
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ)若 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com