
【题目】定义在![]() 上的函数
上的函数![]() ,若已知其在
,若已知其在![]() 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当![]() 时函数取得最大值为
时函数取得最大值为![]() ;当
;当![]() ,函数取得最小值为
,函数取得最小值为![]() .
.
(1)求出此函数的解析式;
(2)若将函数![]() 的图像保持横坐标不变纵坐标变为原来的
的图像保持横坐标不变纵坐标变为原来的![]() 得到函数
得到函数![]() ,再将函数
,再将函数![]() 的图像向左平移
的图像向左平移![]() 个单位得到函数
个单位得到函数![]() ,已知函数
,已知函数![]() 的最大值为
的最大值为![]() ,求满足条件的
,求满足条件的![]() 的最小值;
的最小值;
(3)是否存在实数![]() ,满足不等式
,满足不等式![]() ?若存在,求出
?若存在,求出![]() 的范围(或值),若不存在,请说明理由.
的范围(或值),若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)利用最大值和最小值确定![]() 和
和![]() ,进而得到
,进而得到![]() ;利用
;利用![]() 可求得
可求得![]() 的取值,进而得到所求函数解析式;
的取值,进而得到所求函数解析式;
(2)由图象平移和伸缩变换原则得到![]() ,由
,由![]() 与函数
与函数![]() 的单调性可知只有当
的单调性可知只有当![]() ,
,![]() 同时取得时,函数取最大值,由此可得到
同时取得时,函数取最大值,由此可得到![]() ,根据
,根据![]() 得到最终结果;
得到最终结果;
(3)由偶次根式被开方数大于等于零可确定![]() 的范围,进而得到两角整体所处范围,根据函数单调性可得到
的范围,进而得到两角整体所处范围,根据函数单调性可得到![]() ,解不等式即可求得结果.
,解不等式即可求得结果.
(1)![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
解得:![]() ,
,![]() ,又
,又![]()
![]()
![]()
(2)由题意知:![]() ,
,![]()
![]() 函数
函数![]() 与函数
与函数![]() 均为单调增函数,且
均为单调增函数,且![]() ,
,![]()
![]() 当且仅当
当且仅当![]() 与
与![]() 同时取得才有函数的最大值为
同时取得才有函数的最大值为![]()
由![]() 得:
得:![]() ,
,![]()
又![]()
![]()
![]() ,
,![]()
又![]()
![]() 的最小值为
的最小值为![]()
(3)![]() 满足
满足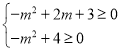 ,解得:
,解得:
![]()
![]()
同理![]()
![]() ,
,![]()
![]() ,
,![]()
由(1)知函数在![]() 上递增
上递增
若有![]()
只需要:![]() ,即
,即![]() 成立即可
成立即可
![]() 存在
存在![]() ,使
,使![]() 成立
成立


科目:高中数学 来源: 题型:
【题目】给定函数y=f(x),设集合A={x|y=f(x)},B={y|y=f(x)}.若对于x∈A,y∈B,使得x+y=0成立,则称函数f(x)具有性质P.给出下列三个函数:①![]() ;②
;②![]() ;③y=lgx.其中,具有性质P的函数的序号是_____.
;③y=lgx.其中,具有性质P的函数的序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]()
(1)当![]() 时,讨论
时,讨论![]() 的单调性
的单调性
(2)当![]() 时,是否存在整数
时,是否存在整数![]() 使得关于
使得关于![]() 的不等式
的不等式![]() 在区间
在区间![]() 内有解?若存在,求出整数
内有解?若存在,求出整数![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-1,![]() (a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是()
(a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点与短轴的一个顶点构成底边为
的两个焦点与短轴的一个顶点构成底边为![]() ,顶角为
,顶角为![]() 的等腰三角形.
的等腰三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 、
、![]() 、
、![]() 是椭圆上三动点,且
是椭圆上三动点,且![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某石化集团获得了某地深海油田区块的开采权.集团在该地区随机初步勘探了部分几口井.取得了地质资料,进入全面勘探时期后.集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高.如果新设计的井位与原有井位重合或接近.便利用旧并的地质资料.不必打这日新并,以节约勘探费与用,勘探初期数据资料见如表:
井号 |
|
|
|
|
|
|
坐标 |
|
|
|
|
|
|
钻探深度 |
|
|
|
|
|
|
出油量 |
|
|
|
|
|
|
(参考公式和计算结果: ,
,![]() ,
,![]() ,
,![]() ).
).
(![]() )
)![]() 号旧井位置线性分布,借助前
号旧井位置线性分布,借助前![]() 组数据求得回归直线方程为
组数据求得回归直线方程为![]() ,求
,求![]() 的值.
的值.
(![]() )现准备勘探新井
)现准备勘探新井![]() ,若通过
,若通过![]() ,
,![]() ,
,![]() ,
,![]() 号井计算出的
号井计算出的![]() ,
,![]() 的值(
的值(![]() ,
,![]() 精确到
精确到![]() )相比于(
)相比于(![]() )中的
)中的![]() ,
,![]() ,值之差不超过
,值之差不超过![]() .则使用位置最接近的已有旧井
.则使用位置最接近的已有旧井![]() .否则在新位置打开,请判断可否使用旧井?
.否则在新位置打开,请判断可否使用旧井?
(![]() )设出油量与勘探深度的比值
)设出油量与勘探深度的比值![]() 不低于
不低于![]() 的勘探井称为优质井,那么在原有
的勘探井称为优质井,那么在原有![]() 口井中任意勘探
口井中任意勘探![]() 口井,求勘探优质井数
口井,求勘探优质井数![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①对于独立性检验,![]() 的值越大,说明两事件相关程度越大,②以模型
的值越大,说明两事件相关程度越大,②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() 的值分别是
的值分别是![]() 和
和![]() ,③某中学有高一学生400人,高二学生300人,高三学生200人,学校团委欲用分层抽样的方法抽取18名学生进行问卷调查,则高一学生被抽到的概率最大,④通过回归直线
,③某中学有高一学生400人,高二学生300人,高三学生200人,学校团委欲用分层抽样的方法抽取18名学生进行问卷调查,则高一学生被抽到的概率最大,④通过回归直线![]() =
=![]()
![]() +
+![]() 及回归系数
及回归系数![]() ,可以精确反映变量的取值和变化趋势,其中正确的个数是
,可以精确反映变量的取值和变化趋势,其中正确的个数是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】打赢扶贫攻坚战,到2020年全面建成小康社会,是中国共产党向全世界和全国人民的承诺.一贫困户在政府扶持下结合地方特色联合当地几户贫困户创办一家农产品公司.为了振兴乡村,打好扶贫攻坚战,某市党政府开展了地标特产展销会.该公司拟定在2020年元旦展销期间举行产品促销活动,经测算该产品的年销量t万件(生产量与销量相等)与促销费用x万元满足![]() 已知2020年生产该产品还需投入成本4+t万元(不含促销费),促销费x满足当
已知2020年生产该产品还需投入成本4+t万元(不含促销费),促销费x满足当![]() 产品销量价格定为5元/件,当
产品销量价格定为5元/件,当![]() 产品销量价格定为
产品销量价格定为![]() 元/件(其中a为正常数).
元/件(其中a为正常数).
(1)试将2020年该产品的利润y万元表示为促销费费x万元的函数;
(2)2020年该公司促销费投入多少万元时,公司利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com