
°æƒø°ø°∞ŒÂ“ª°±∆⁄º‰£¨Œ™¡À¬˙◊„π„¥Û»À√Òµƒœ˚∑—–Ë«Û£¨ƒ≥π≤œÌµ•≥µπ´Àæ”˚Õ∂∑≈“ª≈˙π≤œÌµ•≥µ£¨µ•≥µ◊Ð ˝≤ª≥¨π˝100¡æ£¨œ÷”–A£¨B¡Ω÷÷–Õ∫≈µƒµ•≥µ£∫∆‰÷–A–Õ≥µŒ™‘À∂Ø–Õ£¨≥…±æŒ™400‘™![]() ¡æ£¨∆Ô––∞Ζ° ±–˪®∑—
¡æ£¨∆Ô––∞Ζ° ±–˪®∑—![]() ‘™£ªB–Õ≥µŒ™«·±„–Õ£¨≥…±æŒ™2400‘™
‘™£ªB–Õ≥µŒ™«·±„–Õ£¨≥…±æŒ™2400‘™![]() ¡æ£¨∆Ô––∞Ζ° ±–˪®∑—1‘™
¡æ£¨∆Ô––∞Ζ° ±–˪®∑—1‘™![]() »Ùπ´ÀæÕ∂»Î≥…±æ◊ Ω≤ªƒÐ≥¨π˝8ÕÚ‘™£¨«“Õ∂»Îµƒ≥µ¡æ∆Ωæ˘√ø≥µ√øÃϪ·±ª∆Ô––2¥Œ£¨√ø¥Œ≤ª≥¨π˝∞Ζ° ±
»Ùπ´ÀæÕ∂»Î≥…±æ◊ Ω≤ªƒÐ≥¨π˝8ÕÚ‘™£¨«“Õ∂»Îµƒ≥µ¡æ∆Ωæ˘√ø≥µ√øÃϪ·±ª∆Ô––2¥Œ£¨√ø¥Œ≤ª≥¨π˝∞Ζ° ±![]() ≤ª◊„∞Ζ° ±∞¥∞Ζ° ±º∆À„
≤ª◊„∞Ζ° ±∞¥∞Ζ° ±º∆À„![]() £¨Œ π´Àæ»Á∫ŒÕ∂∑≈¡Ω÷÷–Õ∫≈µƒµ•≥µ≤≈ƒÐ π√øÃϪҵ√µƒ◊Ð ’»Î◊Ó∂ý£¨◊Ó∂ýŒ™∂ý…Ÿ‘™£ø
£¨Œ π´Àæ»Á∫ŒÕ∂∑≈¡Ω÷÷–Õ∫≈µƒµ•≥µ≤≈ƒÐ π√øÃϪҵ√µƒ◊Ð ’»Î◊Ó∂ý£¨◊Ó∂ýŒ™∂ý…Ÿ‘™£ø
°æ¥∞∏°øπ´ÀæÕ∂∑≈¡Ω÷÷–Õ∫≈µƒµ•≥µ∑÷±Œ™80¡æ20¡æ≤≈ƒÐ π√øÃϪҵ√µƒ◊Ð ’»Î◊Ó∂ý£¨◊Ó∂ýŒ™120‘™£Æ
°æΩ‚Œˆ°ø
∏˘æð“‚£¨…ËÕ∂∑≈A–Õ∫≈µ•≥µx¡æ£¨B–Õ∫≈µ•≥µy¡æ£¨µ•≥µπ´Àæø…ªÒµ√µƒ◊Ð ’»ÎŒ™Z£¨ø…µ√µΩ‘º ¯Ãıº˛µƒ Ω◊”£¨º∞ƒø±Í∫Ø ˝![]() £¨ª≠≥ˆ≤ªµ» Ω◊È±Ì æµƒ∆Ω√Ê«¯”Ú£¨µ±ƒø±Í∫Ø ˝
£¨ª≠≥ˆ≤ªµ» Ω◊È±Ì æµƒ∆Ω√Ê«¯”Ú£¨µ±ƒø±Í∫Ø ˝![]() £¨æ≠π˝µ„
£¨æ≠π˝µ„![]() ±£¨
±£¨![]() »°µ√◊Ó¥Û÷µ£¨«ÛΩ‚º¥ø…°£
»°µ√◊Ó¥Û÷µ£¨«ÛΩ‚º¥ø…°£
Ω‚£∫∏˘æð“‚£¨…ËÕ∂∑≈A–Õ∫≈µ•≥µx¡æ£¨B–Õ∫≈µ•≥µy¡æ£¨µ•≥µπ´Àæ√øÃÏø…ªÒµ√µƒ◊Ð ’»ÎŒ™Z£¨
‘Ú”–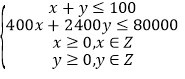 £¨
£¨
º¥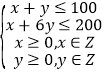 £¨
£¨![]()
«“![]() £¨
£¨
ª≠≥ˆ≤ªµ» Ω◊È![]() ±Ì 浃∆Ω√Ê«¯”Ú£¨”…
±Ì 浃∆Ω√Ê«¯”Ú£¨”…![]() £¨Ω‚µ√
£¨Ω‚µ√![]() .
.
µ±ƒø±Í∫Ø ˝![]() £¨æ≠π˝µ„
£¨æ≠π˝µ„![]() ±£¨
±£¨![]() »°µ√◊Ó¥Û÷µŒ™£∫
»°µ√◊Ó¥Û÷µŒ™£∫![]() .
.

¥£∫π´ÀæÕ∂∑≈¡Ω÷÷–Õ∫≈µƒµ•≥µ∑÷±Œ™80¡æ20¡æ≤≈ƒÐ π√øÃϪҵ√µƒ◊Ð ’»Î◊Ó∂ý£¨◊Ó∂ýŒ™120‘™°£



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ´’˝’˚ ˝1£¨2£¨3£¨![]() £¨n£¨
£¨n£¨![]() ≈≈≥… ˝±Ì»Á±ÌÀ˘ 棨º¥µ⁄“ª––3∏ˆ ˝£¨µ⁄∂˛––6∏ˆ ˝£¨«“∫Û“ª––±»«∞“ª––∂ý3∏ˆ ˝£¨»Ùµ⁄i––£¨µ⁄j¡–µƒ ˝ø…”√
≈≈≥… ˝±Ì»Á±ÌÀ˘ 棨º¥µ⁄“ª––3∏ˆ ˝£¨µ⁄∂˛––6∏ˆ ˝£¨«“∫Û“ª––±»«∞“ª––∂ý3∏ˆ ˝£¨»Ùµ⁄i––£¨µ⁄j¡–µƒ ˝ø…”√![]() ±Ì 棨‘Ú100ø…±Ì 挙______£Æ
±Ì 棨‘Ú100ø…±Ì 挙______£Æ
µ⁄1¡– | µ⁄2¡– | µ⁄3¡– | µ⁄4¡– | µ⁄5¡– | µ⁄6¡– | µ⁄7¡– | µ⁄8¡– |
| |
µ⁄1–– | 1 | 2 | 3 | ||||||
µ⁄2–– | 9 | 8 | 7 | 6 | 5 | 4 | |||
µ⁄3–– | 10/p> | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|
|
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨Àƒ¿‚◊∂![]() ÷–£¨
÷–£¨![]() «’˝»˝Ω«–Œ£¨Àƒ±þ–Œ
«’˝»˝Ω«–Œ£¨Àƒ±þ–Œ![]() «¡‚–Œ£¨µ„
«¡‚–Œ£¨µ„![]() «
«![]() µƒ÷–µ„.
µƒ÷–µ„.

£®I£©«Û÷§£∫![]() // ∆Ω√Ê
// ∆Ω√Ê![]() £ª
£ª
£®II£©»Ù∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £¨
£¨![]() £¨ «Û÷±œþ
£¨ «Û÷±œþ![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() À˘≥…Ω«µƒ’˝œ“÷µ.
À˘≥…Ω«µƒ’˝œ“÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ![]() ÷–£¨∂‘”⁄÷±œþ
÷–£¨∂‘”⁄÷±œþ![]() ∫Õµ„
∫Õµ„![]() °¢
°¢![]() £¨º«
£¨º«![]() £¨»Ù
£¨»Ù![]() £¨‘Ú≥∆µ„
£¨‘Ú≥∆µ„![]() ,
,![]() ±ª÷±œþl∑÷∏Ù£¨»Ù«˙œþC”Î÷±œþl√ª”–π´π≤µ„£¨«“«˙œþC…œ¥Ê‘⁄µ„
±ª÷±œþl∑÷∏Ù£¨»Ù«˙œþC”Î÷±œþl√ª”–π´π≤µ„£¨«“«˙œþC…œ¥Ê‘⁄µ„![]() ,
,![]() ±ª÷±œþl∑÷∏Ù£¨‘Ú≥∆÷±œþlŒ™«˙œþCµƒ“ªÃı∑÷∏Ùœþ.
±ª÷±œþl∑÷∏Ù£¨‘Ú≥∆÷±œþlŒ™«˙œþCµƒ“ªÃı∑÷∏Ùœþ.
£®1£©«Û÷§£∫µ„![]() °¢
°¢![]() ±ª÷±œþ
±ª÷±œþ![]() ∑÷∏Ù£ª
∑÷∏Ù£ª
£®2£©»Ù÷±œþ![]() ««˙œþ
««˙œþ![]() µƒ∑÷∏Ùœþ£¨«Û µ ˝
µƒ∑÷∏Ùœþ£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£ª
µƒ»°÷µ∑∂Œß£ª
£®3£©∂ص„MµΩµ„![]() µƒæý¿Î”εΩy÷·µƒæý¿Î÷ƪ˝Œ™1£¨…˵„MµƒπϺ£Œ™E£¨«ÛEµƒ∑Ω≥ã¨≤¢÷§√˜y÷·Œ™«˙œþEµƒ∑÷∏Ùœþ.
µƒæý¿Î”εΩy÷·µƒæý¿Î÷ƪ˝Œ™1£¨…˵„MµƒπϺ£Œ™E£¨«ÛEµƒ∑Ω≥ã¨≤¢÷§√˜y÷·Œ™«˙œþEµƒ∑÷∏Ùœþ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() £∫
£∫![]() £®
£®![]() £©µƒ◊Û°¢”“Ωπµ„∑÷±Œ™
£©µƒ◊Û°¢”“Ωπµ„∑÷±Œ™![]() £¨π˝µ„
£¨π˝µ„![]() µƒ÷±œþ
µƒ÷±œþ![]() Ωª
Ωª![]() ”⁄
”⁄![]() £¨
£¨![]() ¡Ωµ„£¨
¡Ωµ„£¨![]() µƒ÷Ð≥§Œ™
µƒ÷Ð≥§Œ™![]() £¨
£¨ ![]() µƒ¿Î–ƒ¬
µƒ¿Î–ƒ¬ ![]()
£®¢Ò£©«Û![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®¢Ú£©…˵„![]() £¨
£¨![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() ÷·µƒ¥πœþ
÷·µƒ¥πœþ![]() £¨ ‘≈–∂œ÷±œþ
£¨ ‘≈–∂œ÷±œþ![]() ”Î÷±œþ
”Î÷±œþ![]() µƒΩªµ„ «∑Ò∫„‘⁄“ªÃı∂®÷±œþ…œ£ø»Ù «£¨«Û∏√∂®÷±œþµƒ∑Ω≥ãª∑Ò‘Ú£¨Àµ√˜¿Ì”….
µƒΩªµ„ «∑Ò∫„‘⁄“ªÃı∂®÷±œþ…œ£ø»Ù «£¨«Û∏√∂®÷±œþµƒ∑Ω≥ãª∑Ò‘Ú£¨Àµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £¨∫Ø ˝
£¨∫Ø ˝![]() £Æ
£Æ
£®¢Ò£©«Û∫Ø ˝![]() µƒº´÷µ£ª
µƒº´÷µ£ª
£®¢Ú£©µ±![]() ±£¨÷§√˜£∫∂‘“ª«–µƒ
±£¨÷§√˜£∫∂‘“ª«–µƒ![]() £¨∂º”–
£¨∂º”–![]() ∫„≥…¡¢£ª
∫„≥…¡¢£ª
£®¢Û£©µ±![]() ±£¨∫Ø ˝
±£¨∫Ø ˝![]() £¨
£¨![]() ”–◊Ó–°÷µ£¨º«
”–◊Ó–°÷µ£¨º«![]() µƒ◊Ó–°÷µŒ™
µƒ◊Ó–°÷µŒ™![]() £¨÷§√˜£∫
£¨÷§√˜£∫![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝ £¨»Ù«˙œþ
£¨»Ù«˙œþ![]() …œ º÷’¥Ê‘⁄¡Ωµ„
…œ º÷’¥Ê‘⁄¡Ωµ„![]() £¨ πµ√
£¨ πµ√![]() £¨«“
£¨«“![]() µƒ÷–µ„‘⁄
µƒ÷–µ„‘⁄![]() ÷·…œ£¨‘Ú’˝ µ ˝
÷·…œ£¨‘Ú’˝ µ ˝![]() µƒ»°÷µ∑∂ŒßŒ™£® £©
µƒ»°÷µ∑∂ŒßŒ™£® £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™Õ÷‘≤C£∫![]() µƒ¿Î–ƒ¬ Œ™
µƒ¿Î–ƒ¬ Œ™![]() £¨≤¢«“Õ÷‘≤æ≠π˝µ„P(1£¨
£¨≤¢«“Õ÷‘≤æ≠π˝µ„P(1£¨![]() )£¨÷±œþlµƒ∑Ω≥ÃŒ™x£Ω4£Æ
)£¨÷±œþlµƒ∑Ω≥ÃŒ™x£Ω4£Æ
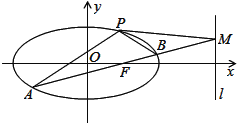
£®1£©«ÛÕ÷‘≤µƒ∑Ω≥ãª
£®2£©“—÷™Õ÷‘≤ƒ⁄“ªµ„E(1£¨0)£¨π˝µ„E◊˜“ªÃı–±¬ Œ™kµƒ÷±œþ”ÎÕ÷‘≤Ωª”⁄A£¨B¡Ωµ„£¨Ωª÷±œþl”⁄µ„M£¨º«PA£¨PB£¨PMµƒ–±¬ ∑÷±Œ™k1£¨k2£¨k3£ÆŒ £∫ «∑ҥʑ⁄≥£ ˝![]() £¨ πµ√k1£´k2£Ω
£¨ πµ√k1£´k2£Ω![]() k3£ø»Ù¥Ê‘⁄£¨«Û≥ˆ
k3£ø»Ù¥Ê‘⁄£¨«Û≥ˆ![]() µƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝ f£®x£©=ax+£®1©Åa£©lnx+![]() £®a° R£©
£®a° R£©
£®¢Ò£©µ±a=0 ±£¨«Û f£®x£©µƒº´÷µ£ª
£®¢Ú£©µ±a£º0 ±£¨«Û f£®x£©µƒµ•µ˜«¯º‰£ª
£®¢Û£©∑Ω≥à f£®x£©=0µƒ∏˘µƒ∏ˆ ˝ƒÐ∑Ò¥ÔµΩ3£¨»ÙƒÐ«Î«Û≥ˆ¥À ±aµƒ∑∂Œß£¨»Ù≤ªƒÐ£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com