
【题目】已知函数f(x)=ax+ ![]() +2﹣2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.
+2﹣2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.
(1)求a,b满足的关系式;
(2)若f(x)≥2lnx在[1,+∞)上恒成立,求a的取值范围;
(3)证明:1+ ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() (2n+1)+
(2n+1)+ ![]() (n∈N*).
(n∈N*).
【答案】
(1)解:函数的导数为f′(x)=a﹣ ![]() ,
,
因为f(x)=ax+ ![]() +2﹣2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.
+2﹣2a(a>0)的图象在点(1,f(1))处的切线与直线y=2x+1平行.
所以f'(1)=2,即f'(1)=a﹣b=2,所以b=a﹣2
(2)解:因为b=a﹣2,所以f(x)=ax+ ![]() +2﹣2a,
+2﹣2a,
若f(x)≥2lnx,则f(x)﹣2lnx≥0,
设g(x)=f(x)﹣2lnx=ax+ ![]() +2﹣2a﹣2lnx,x∈[1,+∞).
+2﹣2a﹣2lnx,x∈[1,+∞).
则g(1)=0,g′(x)= ![]() ,
,
①当0<a<1时, ![]() >1,若1<x<
>1,若1<x< ![]() ,则g'(x)<0,
,则g'(x)<0,
此时g(x)在[1,+∞)上单调递减,所以g(x)<g(1)=0,
即f(x)≥2lnx在[1,+∞)不恒成立.
②若a≥1, ![]() ≤1,当x>1时,g'(x)>0,g(x)在[1,+∞)上单调递增,
≤1,当x>1时,g'(x)>0,g(x)在[1,+∞)上单调递增,
又g(1)=0,所以此时f(x)≥2lnx.
综上所述,所求a的取值范围是[1,+∞)
(3)证明:由(2)知当a≥1时,f(x)≥2lnx在[1,+∞)上恒成立.
取a=1得x﹣ ![]() ≥2lnx
≥2lnx
令x= ![]() >1,得
>1,得 ![]() ﹣
﹣ ![]() >2ln
>2ln ![]() ,
,
即 ![]() ﹣
﹣ ![]() >ln
>ln ![]() ,
,
所以 ![]() >
> ![]() ln
ln ![]() +
+ ![]() (
( ![]() ﹣
﹣ ![]() )
)
上式中n=1,2,3,…,n,然后n个不等式相加得1+ ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() (2n+1)+
(2n+1)+ ![]()
【解析】(1)利用函数在点(1,f(1))处的切线与直线y=2x+1平行,得到f'(1)=2,然后利用导数确定a,b满足的关系式.(2)构造函数g(x)=f(x)﹣2lnx=ax+ ![]() +2﹣2a﹣2lnx,x∈[1,+∞).利用导数求函数的最值即可.(3)取a=1得x﹣
+2﹣2a﹣2lnx,x∈[1,+∞).利用导数求函数的最值即可.(3)取a=1得x﹣ ![]() ≥2lnx,令x=
≥2lnx,令x= ![]() >1,得
>1,得 ![]() >
> ![]() ln
ln ![]() +
+ ![]() (
( ![]() ﹣
﹣ ![]() ),上式中n=1,2,3,…,n,然后n个不等式相加得结论.
),上式中n=1,2,3,…,n,然后n个不等式相加得结论.


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn+an=4,n∈N*
(1)求数列{an}的通项公式;
(2)已知cn=2n+3(n∈N*),记dn=cn+logCan(C>0,C≠1),是否存在这样的常数C,使得数列{dn}是常数列,若存在,求出C的值;若不存在,请说明理由.
(3)若数列{bn},对于任意的正整数n,均有 ![]() 成立,求证:数列{bn}是等差数列.
成立,求证:数列{bn}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,上海迪士尼乐园将一三角形地块ABC的一角APQ开辟为游客体验活动区.已知∠A=120°,AB、AC的长度均大于200米.设AP=x,AQ=y,且AP,AQ总长度为200米. 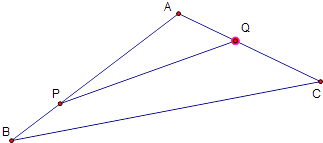
(1)当x,y为何值时?游客体验活动区APQ的面积最大,并求最大面积;
(2)当x,y为何值时?线段|PQ|最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场对顾客实行购物优惠活动,规定一次购物付款总额:
(1)如果不超过200元,则不给予优惠;
(2)如果超过200元但不超过500元,则按标价给予9折优惠;
(3)如果超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予7折优惠.
某人单独购买A,B商品分别付款168元和423元,假设他一次性购买A,B两件商品,则应付款是
A. 413.7元 B. 513.7元 C. 546.6元 D. 548.7元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是(﹣1,1)上的偶函数,且在区间(﹣1,0)上是单调递增的,A,B,C是锐角三角形△ABC的三个内角,则下列不等式中一定成立的是( )
A.f(sinA)>f(sinB)
B.f(sinA)>f(cosB)
C.f(cosC)>f(sinB)
D.f(sinC)>f(cosB)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运输队接到给灾区运送物资的任务,该运输队有8辆载重为![]() 的
的![]() 型卡车,6辆载重为
型卡车,6辆载重为![]() 的
的![]() 型卡车,10名驾驶员,要求此运输队每天至少运送
型卡车,10名驾驶员,要求此运输队每天至少运送![]() 救灾物资.已知每辆卡车每天往返的次数为
救灾物资.已知每辆卡车每天往返的次数为![]() 型卡车16次,
型卡车16次, ![]() 型卡车12次.每辆卡车每天往返的成本为
型卡车12次.每辆卡车每天往返的成本为![]() 型卡车240元,
型卡车240元, ![]() 型卡车378元.问每天派出
型卡车378元.问每天派出![]() 型卡车与
型卡车与![]() 型卡车各多少辆,运输队所花的成本最低?
型卡车各多少辆,运输队所花的成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某几何体的三视图如图所示,且该几何体的体积是3,则正视图的![]() 的值__________.
的值__________.

【答案】3
【解析】 由已知中的三视图可得该几何体是一个以直角梯形为底面,梯形上下边长为![]() 和
和![]() ,高为
,高为![]() ,
,
如图所示, ![]() 平面
平面![]() ,
,
所以底面积为![]() ,
,
几何体的高为![]() ,所以其体积为
,所以其体积为![]() .
.

点睛:在由三视图还原为空间几何体的实际形状时,要从三个视图综合考虑,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线.在还原空间几何体实际形状时,一般是以正视图和俯视图为主,结合侧视图进行综合考虑.求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解.
【题型】填空题
【结束】
16
【题目】已知椭圆![]() :
: ![]() 的右焦点为
的右焦点为![]() ,
, ![]() 为直线
为直线![]() 上一点,线段
上一点,线段![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为2,离心率为
的短轴长为2,离心率为![]()
(1)求椭圆C的方程;
(2)设过点M(2,0)的直线l与椭圆C相交于A,B两点,F1为椭圆的左焦点.
①若B点关于x轴的对称点是N,证明:直线AN恒过一定点;
②试求椭圆C上是否存在点P,使F1APB为平行四边形?若存在,求出F1APB的面积,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com