【题目】某健康社团为调查居民的运动情况，统计了某小区100名居民平均每天的运动时长（单位：小时）并根据统计数据分为
六个小组（所调查的居民平均每天运动时长均在
内），得到的频率分布直方图如图所示.
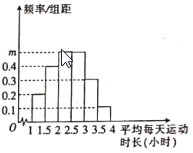
（1）求出图中
的值，并估计这
名居民平均每天运动时长的平均值及中位数（同一组中的每个数据可用该组区间的中点值代替）；
（2）为了分析出该小区居民平均每天的运动量与职业、年龄等的关系，该社团按小组用分层抽样的方法抽出20名居民进一步调查，试问在
时间段内应抽出多少人？
科目：高中数学 来源： 题型：
【题目】为了庆祝中华人民共和国成立
周年，某车间内举行生产比赛，由甲乙两组内各随机选取
名技工，在单位时间生产同一种零件，其生产的合格零件数的茎叶图如下：
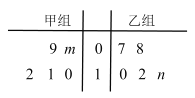
已知两组所选技工生产的合格零件的平均数均为
.
（1）分别求出
的值；
（2）分别求出甲乙两组技工在单位时间内加工的合格零件的方差
和
,并由此估计两组技工的生产水平；
（3）若单位时间内生产的合格零件个数不小于平均数的技工即为“生产能手”，根据以上数据，能否认为该车间50%以上的技工都是生产能手？
(注：方差
,其中
为数据
的平均数).
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝ax＋x2，g(x)＝xlna，a>1.
(1)求证：函数F(x)＝f(x)－g(x)在(0，＋∞)上单调递增；
(2)若函数y＝
－3有四个零点，求b的取值范围；
(3)若对于任意的x1，x2∈[－1,1]时，都有|F(x2)－F(x1)|≤e2－2恒成立，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若函数
在区间
上， 
， 
， 
， 
， 
， 
均可为一个三角形的三边长，则称函数
为“三角形函数”．已知函数
在区间
上是“三角形函数”，则实数
的取值范围为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）
与g（x）＝3elnx+mx的图象有4个不同的交点，则实数m的取值范围是（ ）
A.（﹣3，
）B.（﹣1，）C.（﹣1，3）D.（0，3）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在极坐标系中，直线的方程为2ρcosθ+5ρsinθ﹣8＝0，曲线E的方程为ρ＝4cosθ．
（1）以极点O为直角坐标原点，极轴为x轴正半轴建立平面直角坐标系，分别写出直线l与曲线E的直角坐标方程；
（2）设直线l与曲线E交于A，B两点，点C在曲线E上，求△ABC面积的最大值，并求此时点C的直角坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设f（x）＝loga（1+x）+loga（3﹣x）（a＞0，a≠1）且f（1）＝2．
（1）求a的值及f（x）的定义域；
（2）求f（x）在区间[0,
]上的最大值和最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者，从符合条件的500名志愿者中随机抽样100名志原者的年龄情况如下表所示．
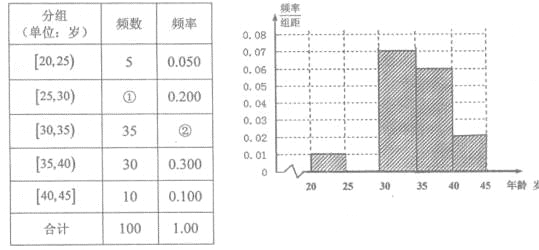
（Ⅰ）频率分布表中的①、②位置应填什么数据？并在答题卡中补全频率分布直方图（如图），再根据频率分布直方图估计这500名志愿者中年龄在
岁的人数；
（Ⅱ）在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加中心广场的宣传活动，从这20人中选取2名志愿者担任主要负责人，记这2名志愿者中“年龄低于30岁”的人数为
，求的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
