
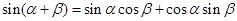 ------①
------①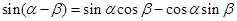 ------②
------②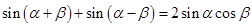 ------③
------③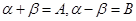 有
有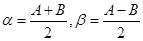
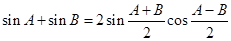 .
. ;
;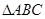 的三个内角
的三个内角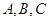 满足
满足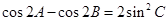 ,试判断
,试判断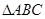 的形状.
的形状.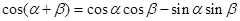 , ①
, ①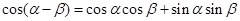 , ② 2分
, ② 2分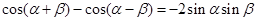 . ③ 3分
. ③ 3分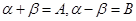 有
有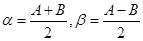 ,
,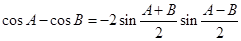 . 6分
. 6分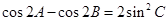 可化为
可化为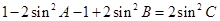 , 8分
, 8分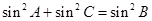 . 9分
. 9分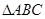 的三个内角A,B,C所对的边分别为
的三个内角A,B,C所对的边分别为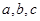 ,
,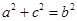 . 11分
. 11分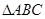 为直角三角形. 12分
为直角三角形. 12分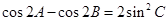 可化为
可化为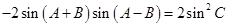 , 8分
, 8分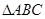 的内角,所以
的内角,所以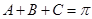 ,
,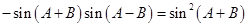 .
.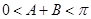 ,所以
,所以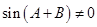 ,
,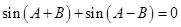 .
.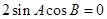 . 10分
. 10分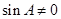 ,所以
,所以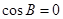 ,即
,即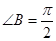 .
.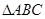 为直角三角形. 12分
为直角三角形. 12分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com