
(本题满分13分)已知抛物线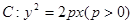 过点
过点 。
。
(1)求抛物线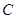 的标准方程,并求其准线方程;
的标准方程,并求其准线方程;
(2)是否存在平行于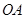 (
(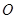 为坐标原点)的直线
为坐标原点)的直线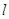 ,使得直线
,使得直线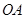 与
与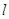 的距离等于
的距离等于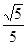 ?
?
若存在,求直线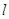 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
(3)过抛物线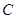 的焦点
的焦点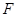 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线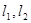 ,设
,设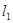 与抛物线
与抛物线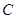 相交于点
相交于点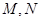 ,
, 与抛物线
与抛物线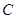 相交于点
相交于点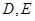 ,求
,求 的最小值。
的最小值。
(1) 抛物线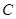 的方程为
的方程为 ,其准线方程为
,其准线方程为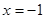 (2)
符合题意的直线
(2)
符合题意的直线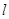 存在,其方程为
存在,其方程为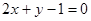 (3)
(3)
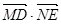 的最小值为16.
的最小值为16.
【解析】
试题分析:(1)将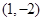 带入
带入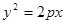 ,得
,得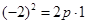 ,所以
,所以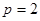 ,
,
故所求抛物线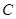 的方程为
的方程为 ,其准线方程为
,其准线方程为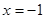 . ……2分
. ……2分
(2)假设存在符合题意的直线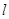 ,其方程为
,其方程为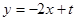 ,
,
由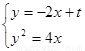 得
得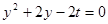 , ……3分
, ……3分
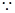 直线
直线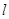 与抛物线
与抛物线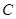 有公共点,
有公共点,
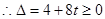 解得
解得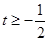 , ……4分
, ……4分
由直线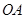 与
与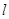 的距离
的距离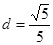 可得
可得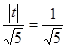 ,解得
,解得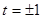 , ……5分
, ……5分
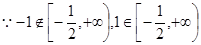 ,
,
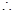 符合题意的直线
符合题意的直线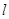 存在,其方程为
存在,其方程为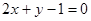 . ……7分
. ……7分
(3)由题意知,直线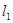 的斜率存在且不为0,设为
的斜率存在且不为0,设为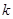 ,则
,则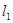 的方程为
的方程为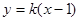 ,
,
由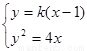 ,得
,得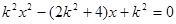 ,
,
设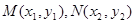 ,则
,则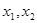 是上述方程的两个实根,
是上述方程的两个实根,
于是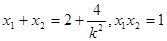 ,
,
因为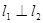 ,所以斜率为
,所以斜率为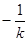 ,
,
设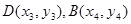 ,则同理可得
,则同理可得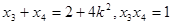 。
。
故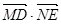 =
=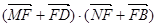 =
=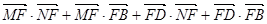
=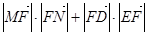 =
=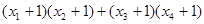
=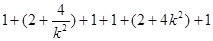
= ,
,
当且仅当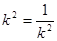 ,即
,即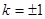 时
时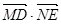 取最小值
取最小值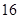 . ……13分
. ……13分
考点:本小题主要考查双曲线标准方程的求法和直线与双曲线的位置关系的应用以及平面向量的坐标运算、基本不等式的应用等,考查学生综合运用所学知识解决问题的能力和运算求解能力.
点评:直线与圆锥曲线的位置关系问题是高考考查的重点内容,且一般出在压轴题的位置,难度较大,主要是运算量较大,所以要充分利用数形结合思想的应用,尽量简化运算.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源:2012-2013学年湖北省八市高三3月联考理科数学试卷(解析版) 题型:解答题
(本题满分13分)已知△ 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.
(Ⅰ)求顶点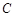 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 为何种圆锥曲线;
为何种圆锥曲线;
(Ⅱ)当 时,过点
时,过点 的直线
的直线 交曲线
交曲线 于
于 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高一上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分13分)已知函数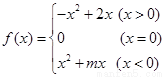 为奇函数;
为奇函数;
(1)求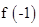 以及m的值;
以及m的值;
(2)在给出的直角坐标系中画出 的图象;
的图象;

(3)若函数 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011年湖南省高三第一次学情摸底考试数学卷 题型:解答题
(本题满分13 分)
已知函数
(1)若在 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值;
(2)若 在区间(-2,3)内有两个不同的极值点,求a 取值范围;
在区间(-2,3)内有两个不同的极值点,求a 取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数 的图象与函数
的图象与函数 的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届江西省高一第二学期入学考试数学 题型:解答题
.(本题满分13分)已知圆C: 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
l交圆C于A、B两点.
(1) 当l经过圆心C时,求直线l的方程;
(2) 当弦AB被点P平分时,写出直线l的方程;
(3) 当直线l的倾斜角为45º时,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源:2012届安徽省六校教育研究会高二素质测试理科数学 题型:解答题
(本题满分13分)已知圆C:
(1)若平面上有两点A(1 , 0),B(-1 , 0),点P是圆C上的动点,求使 取得最小值时点P的坐标.
取得最小值时点P的坐标.
(2) 若 是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆 于
于 两点
两点
①若 ,求直线
,求直线 的方程;
的方程;
②求证:直线 恒过一定点.
恒过一定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com