
分析 (1)直线y=3x+3关于点M(3,2)对称的直线l的方程,可以利用坐标转化方法解答,即设对称的直线上的任意一点为(x,y),关于(3,2)的对称点(6-x,4-y)在直线y=3x+3上,从而求对称的直线方程;
(2)设P(x,y)为所求直线上的任意一点,则P关于直线x+y+2=0对称点P′(x′,y′)在直线y=3x+3,由对称性可解得$\left\{\begin{array}{l}x′=-y-2\\ y′=-x-2\end{array}\right.$,代入变形可得答案.
解答 解:设所求直线上的任意点坐标(x,y)关于点M(3,2)对称点(6-x、4-y),
因为对称点在已知直线上,
所以将y=3x+3中的x、y分别代以(6-x)、(4-y),得4-y=3(6-x)+3,
即3x-y-17=0.
(2)设P(x,y)为所求直线上的任意一点,
则P关于直线x+y+2=0对称点P′(x′,y′)在直线y=3x+3,
∴必有y′=3x′+3 (*)
由对称性可得$\left\{\begin{array}{l}\frac{x+x′}{2}+\frac{y+y′}{2}+2=0\\ \frac{y-y′}{x-x′}=1\end{array}\right.$,解得$\left\{\begin{array}{l}x′=-y-2\\ y′=-x-2\end{array}\right.$,
代入(*)式可得(-x-2)=3(-y-2)+3
化简可得x-3y-1=0,
∴所求对称直线的方程为:x-3y-1=0;
故答案为:3x-y-17=0,x-3y-1=0
点评 本题解答方法较多,可以利用中点坐标转移到所求直线上,也可以按照求轨迹方程方法解答;还可以求一点和斜率来解.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
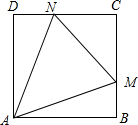 如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )
如图,正万形ABCD的边长为2,M,N分别为边BC、CD上的动点,且∠MAN=45°,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的最小值为( )| A. | 4($\sqrt{2}$-1) | B. | 8($\sqrt{2}$-1) | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方程$\frac{y}{x-2}=1$表示斜率为1,在y轴上截距为-2的直线 | |
| B. | △ABC的三个顶点是A(-3,0),B(3,0),C(0,3),则中线CO(O为坐标原点)的方程是x=0 | |
| C. | 到y轴距离为2的点的轨迹方程为x=2 | |
| D. | 方程y=$\sqrt{{x}^{2}+2x+1}$表示两条射线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com