
(1)如下图所示,设AB、CD是夹在两个平行平面α、β之间的异面直线段,M、N分别为AB、CD的中点,求证:MN∥α.

(2)在本例中,若AB、AE是夹在两个平行平面α、β之间的两条相交线段,且M、N分别为AB、AE的中点,如何证明MN∥α?
|
(1)证法一:过点A作AE∥CD,交α于点E,∵α∥β,则AE 设P为AE的中点,连结PN、PM、BE,则PN∥ED,MP∥BE. 又∵PN 同理,可得PM∥α. 又∵PM∩PN=P,∴平面PMN∥平面α. 又MN 证法二:如下图所示,连结AD,取AD的中点Q,连结QM、QN,
∵Q、N分别为AD、CD的中点,∴QN∥AC. ∵QN ∴QN∥β.∵α∥β,QN∥β,QN ∴QN∥α.同理可证QM∥α. ∵QM∩QN=Q,∴平面QMN∥α. ∵MN ∴MN∥α. (2)证明:连结BE,∵M、N分别是AB、AE的中点, ∴MN∥BE. 又∵MN 思路分析:(1)本题考查两个平面平行的判定方法.要证明MN∥α,由于AB、CD为异面直线,所以要在α内找一条直线,证明它与MN平行较为困难.因此可转化为证明过MN的一个平面与平面α平行. |
|
本题的证法较多,解题关键是如何处理好条件:AB、CD是两条异面线段.证法一实质上是把CD在两平行平面间沿着同一方向移到AE位置,AB和AE可确定一平面,借助于平面几何来处理问题;证法二是借助于空间四边形的对角线AD,把AB和CD分别放在两相交平面内来研究.本题还可以连结CM延长交α于点R,证明MN∥RD即可. |


科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:044
用一块钢锭浇铸一个厚度均匀,且全面积为2平方米的正四棱锥形有盖容器(如下图所示),设容器的高为h米,盖子边长为a米.

(1)求a关于h的函数解析式;
(2)设容器的容积为V立方米,则当h为何值时,V最大?求出V的最大值(不计容器厚度).
查看答案和解析>>
科目:高中数学 来源:湖南省2007届高三十校联考第一次考试理科数学试卷 题型:044
把正整数按上小下大,左小右大的原则排成三角形数表示(每一行比上一行多一个数),如下图所示:设![]() 是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,如a42=8.
是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,如a42=8.

(1)若aij=2007,求i,j的值;
(2)记三角形数表从上往下数第n行各数之和为bn,令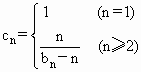 ,若数列{cn}的前n项和为Tn,求
,若数列{cn}的前n项和为Tn,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:

(2)如下图所示,设O是正六边形ABCDEF的中心.在图里的向量中

①写出与![]() 相等的向量;
相等的向量;
②写出与![]() 相等的向量;
相等的向量;
③写出与![]() 共线的向量;
共线的向量;
④写出与![]() 长度相等但方向相反的向量.
长度相等但方向相反的向量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com