
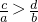 ,命题q:
,命题q: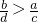 .则命题p是命题q的
.则命题p是命题q的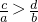 ?
?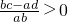 ,命题q:
,命题q: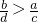 ?
?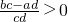 .再结合abcd>0及充分条件必要条件的定义对两个命题的结论进行探究得到正确选项.
.再结合abcd>0及充分条件必要条件的定义对两个命题的结论进行探究得到正确选项.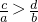 ?
?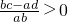 ,命题q:
,命题q: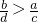 ?
?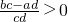 .
.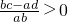 一定有
一定有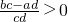 成立,
成立,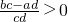 一定有
一定有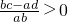 成立,
成立,

科目:高中数学 来源: 题型:
| a |
| x |
| y2 |
| a2 |
查看答案和解析>>
科目:高中数学 来源:温州一模 题型:单选题
| c |
| a |
| d |
| b |
| b |
| d |
| a |
| c |
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2005年浙江省温州市高考数学一模试卷(解析版) 题型:选择题
 ,命题q:
,命题q: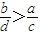 .则命题p是命题q的( )
.则命题p是命题q的( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com