
【题目】如图,椭圆![]() 的左、右顶点分别为A、B,双曲线
的左、右顶点分别为A、B,双曲线![]() 以A、B为顶点,焦距为
以A、B为顶点,焦距为![]() ,点P是
,点P是![]() 上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为
上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为![]()
![]() 为坐标原点.
为坐标原点.
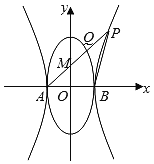
(1)求双曲线![]() 的方程;
的方程;
(2)求点M的纵坐标![]() 的取值范围;
的取值范围;
(3)是否存在定直线![]() 使得直线BP与直线OM关于直线
使得直线BP与直线OM关于直线![]() 对称?若存在,求直线
对称?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】已知函数 的值域是
的值域是![]() ,有下列结论:①当
,有下列结论:①当![]() 时,
时,![]() ; ②当
; ②当![]() 时,
时,![]() ;③当
;③当![]() 时,
时,![]() ; ④当
; ④当![]() 时,
时,![]() .其中结论正确的所有的序号是( ).
.其中结论正确的所有的序号是( ).
A.①②B.③④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,焦点为
上,焦点为![]() ,圆O的直径为
,圆O的直径为![]() .
.

(1)求椭圆C及圆O的标准方程;
(2)设直线l与圆O相切于第一象限内的点P,且直线l与椭圆C交于![]() 两点.记
两点.记![]() 的面积为
的面积为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国已进入新时代中国特色社会主义时期,人民生活水平不断提高.某市随机统计了城区若干户市民十月人均生活支出比九月人均生活支出增加量(记为P元)的情况,并根据统计数据制成如图频率分布直方图.
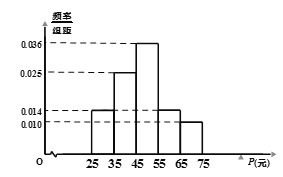
(1)根据频率分布直方图估算P的平均值![]() ;
;
(2)若该市城区有4户市民十月人均生活支出比九月人均生活支出分别增加了42元,50元,52元,60元,从这4户中随机抽取2户,求这2户P值的和超过100元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如下图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(1)不改变车票价格,减少支出费用;建议(2)不改变支出费用,提高车票价格.下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
的函数关系如下图所示(收支差额=车票收入-支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(1)不改变车票价格,减少支出费用;建议(2)不改变支出费用,提高车票价格.下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )

A.①反映建议(2),③反映建议(1)B.①反映建议(1),③反映建议(2)
C.②反映建议(1),④反映建议(2)D.④反映建议(1),②反映建议(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() 且满足
且满足![]() ,
,![]() (
(![]() 为常数,
为常数,![]() ).
).
(1)求![]() ;
;
(2)若数列![]() 是等比数列,求实数
是等比数列,求实数![]() 的值;
的值;
(3)是否存在实数![]() ,使得数列
,使得数列![]() 满足:可以从中取出无限多项并按原来的先后次序排成一个等差数列?若存在,求出所有满足条件的值;若不存在,请说明理由.
满足:可以从中取出无限多项并按原来的先后次序排成一个等差数列?若存在,求出所有满足条件的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com