
设三角形ABC的内角 所对的边长分别为
所对的边长分别为 ,
,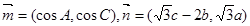 ,且
,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若AC=BC,且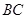 边上的中线
边上的中线 的长为
的长为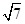 ,求
,求 的面积.
的面积.
(Ⅰ)A= ;(Ⅱ)
;(Ⅱ)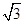
解析试题分析:(Ⅰ)由 可得
可得 通过三角运算即sin(A+C)=sinB.可求得角A的值.
通过三角运算即sin(A+C)=sinB.可求得角A的值.
(Ⅱ)由角A= .可求得C=
.可求得C=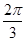 .又因为AC=2CM.即AM=
.又因为AC=2CM.即AM= 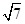 .在三角形AMC中可求得AC的长.再用三角形面积公式即可求得三角形的面积.本题是利用向量垂直知识来求得角A.再根据等腰三角形的内角关系,利用余弦定理求得三角形的面积.
.在三角形AMC中可求得AC的长.再用三角形面积公式即可求得三角形的面积.本题是利用向量垂直知识来求得角A.再根据等腰三角形的内角关系,利用余弦定理求得三角形的面积.
试题解析:(1)由
 1分
1分
所以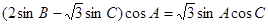 2分
2分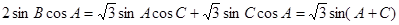
则2sinBcosA= sinB 4分
sinB 4分
所以cosA= 于是A=
于是A= 6分
6分
(2)由(1)知A= ,又AC=BC,所以C=
,又AC=BC,所以C=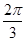 7分
7分
设AC=x,则MC= ,AM=
,AM=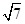 ,在
,在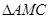 中,由余弦定理得
中,由余弦定理得 9分
9分
即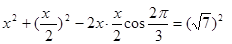
解得x=2 11分
故 13分
13分
考点:1.向量的垂直坐标形式的表示.2.余弦定理.3.三角恒等变换.


科目:高中数学 来源: 题型:解答题
如图,甲船以每小时 海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于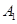 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西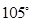 方向的
方向的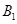 处,此时两船相距
处,此时两船相距 海里,当甲船航行
海里,当甲船航行 分钟到达
分钟到达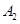 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西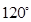 方向的
方向的 处,此时两船相距
处,此时两船相距 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com