
【题目】已知函数![]() 的图象在点
的图象在点![]() 处的切线斜率为
处的切线斜率为![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)求实数![]() 的值,并求
的值,并求![]() 的单调区间;
的单调区间;
(2)证明:![]() .
.
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】甲、乙、丙3人站到共有6级的台阶上,若每级台阶最多站2人,同一级台阶上的人不区分站的位置,则不同的站法总数是( )
A.90B.120C.210D.216
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,上顶点为M,过点M且斜率为
,上顶点为M,过点M且斜率为![]() 的直线与
的直线与![]() 交于另一点N,过原点的直线l与
交于另一点N,过原点的直线l与![]() 交于P,Q两点
交于P,Q两点
(1)求![]() 周长的最小值:
周长的最小值:
(2)是否存在这样的直线,使得与直线![]() 平行的弦的中点都在该直线上?若存在,求出该直线的方程:若不存在,请说明理由.
平行的弦的中点都在该直线上?若存在,求出该直线的方程:若不存在,请说明理由.
(3)直线l与线段![]() 相交,且四边形
相交,且四边形![]() 的面积
的面积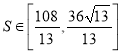 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了提高生产线的运行效率,工厂对生产线的设备进行了技术改造.为了对比技术改造后的效果,采集了生产线的技术改造前后各20次连续正常运行的时间长度(单位:天)数据,并绘制了如下茎叶图:
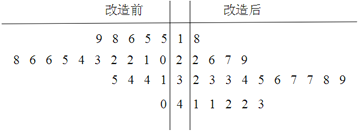
(Ⅰ)(1)设所采集的40个连续正常运行时间的中位数![]() ,并将连续正常运行时间超过
,并将连续正常运行时间超过![]() 和不超过
和不超过![]() 的次数填入下面的列联表:
的次数填入下面的列联表:
超过 | 不超过 | |
改造前 |
|
|
改造后 |
|
|
试写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)根据(1)中的列联表,能否有![]() 的把握认为生产线技术改造前后的连续正常运行时间有差异?
的把握认为生产线技术改造前后的连续正常运行时间有差异?
附: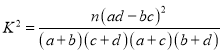 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(Ⅱ)工厂的生产线的运行需要进行维护.工厂对生产线的生产维护费用包括正常维护费、保障维护费两种对生产线设定维护周期为![]() 天(即从开工运行到第
天(即从开工运行到第![]() 天(
天(![]() )进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元
)进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为0.5万元![]() 次;保障维护费第一次为0.2万元
次;保障维护费第一次为0.2万元![]() 周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:
周期,此后每增加一次则保障维护费增加0.2万元.现制定生产线一个生产周期(以120天计)内的维护方案:![]() ,
,![]() ,2,3,4.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
,2,3,4.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,P是上底面A1B1C1D1内一点,若AP∥平面BDEF,则线段AP长度的取值范围是( )
A.[![]() ,
,![]() ]B.[
]B.[![]() ,
,![]() ]C.[
]C.[![]() ,
,![]() ]D.[
]D.[![]() ,
,![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则下列判断正确的是( )
,则下列判断正确的是( )
A.函数![]() 的最小正周期为
的最小正周期为![]() ,在
,在![]() 上单调递增
上单调递增
B.函数![]() 的最小正周期为
的最小正周期为![]() ,在
,在![]() 上单调递增
上单调递增
C.函数![]() 的最小正周期为
的最小正周期为![]() ,在
,在![]() 上单调递增
上单调递增
D.函数![]() 的最小正周期为
的最小正周期为![]() ,在
,在![]() 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市积极贯彻落实国务院《“十三五”节能减排综合工作方案》,空气质量明显改善.该市生态环境局统计了某月(30天)空气质量指数,绘制成如下频率分布直方图.已知空气质量等级与空气质量指数对照如下表:
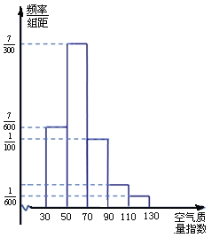
空气质量指数 |
|
|
|
|
| 300以上 |
空气质量等级 | 一级 (优) | 二级 (良) | 三级 (轻度污染) | 四级 (中度污染) | 五级 (重度污染) | 六级 (严重污染) |
(1)根据频率分布直方图估计,在这30天中,空气质量等级为优或良的天数;
(2)根据体质检查情况,医生建议:当空气质量指数高于90时,市民甲不宜进行户外体育运动;当空气质量指数高于70时,市民乙不宜进行户外体育运动(两人是否进行户外体育运动互不影响).
①从这30天中随机选取2天,记乙不宜进行户外体育运动,且甲适宜进行户外体育运动的天数为X,求X的分布列和数学期望;
②以该月空气质量指数分布的频率作为以后每天空气质量指数分布的概率(假定每天空气质量指数互不影响),甲、乙两人后面分别随机选择3天和2天进行户外体育运动,求甲恰有2天,且乙恰有1天不宜进行户外体育运动的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsinθ=2.
(1)M为曲线C1上的动点,点P在线段OM上,且满足![]() ,求点P的轨迹C2的直角坐标方程;
,求点P的轨迹C2的直角坐标方程;
(2)曲线C2上两点![]() 与点B(ρ2,α),求△OAB面积的最大值.
与点B(ρ2,α),求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节前后,一场突如其来的新冠肺炎疫情在全国蔓延.疫情就是命令,防控就是责任.在党中央的坚强领导和统一指挥下,全国人民众志成城、团结一心,掀起了一场坚决打赢疫情防控阻击战的人民战争.下侧的图表展示了2月14日至29日全国新冠肺炎疫情变化情况,根据该折线图,下列结论正确的是( )
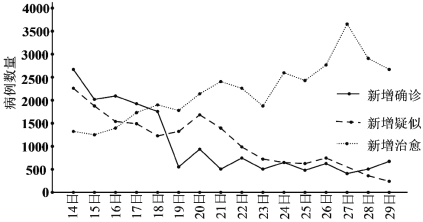
A.16天中每日新增确诊病例数量呈下降趋势且19日的降幅最大
B.16天中每日新增确诊病例的中位数大于新增疑似病例的中位数
C.16天中新增确诊、新增疑似、新增治愈病例的极差均大于![]()
D.19日至29日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com