
分析 根据a1=$\frac{1}{2}$,an+bn=1,先求得b1的值,再根据bn+1=bn+1=$\frac{{b}_{n}}{1-{{a}_{n}}^{2}}$,得到bn+1与bn的递推关系,根据bn+1与bn的递推关系,构造数列{$\frac{1}{{b}_{n}-1}$},利用等差数列的定义,数列{$\frac{1}{{b}_{n}-1}$}是以-2为首项,-1为公差的等差数列,即可求出表达式
解答 解:∵a1=$\frac{1}{2}$,a1+b1=1,an+bn=1
∴b1=$\frac{1}{2}$,an=1-bn,
∴bn+1=$\frac{{b}_{n}}{1-{{a}_{n}}^{2}}$=$\frac{{b}_{n}}{1-(1-{b}_{n})^{2}}$=$\frac{1}{2-{b}_{n}}$
∴$\frac{1}{{b}_{n+1}-1}$-$\frac{1}{{b}_{n}-1}$=-1
∵$\frac{1}{{b}_{1}-1}$=-2,
∴数列{$\frac{1}{{b}_{n}-1}$}是以-2为首项,-1为公差的等差数列,
∴$\frac{1}{{b}_{n}-1}$=-2-(n-1)=-n-1,
∴bn=$\frac{n}{n+1}$,
故答案为:$\frac{n}{n+1}$
点评 本题考查了等差数列的应用,以及构造新数列求通项公式.属中档题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)<f(1)<f(3) | B. | f(2)<f(3)<f(-4) | C. | f(-2)<f(0)<f(1) | D. | f(5)<f(-3)<f(-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
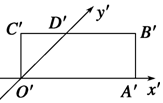 如图,矩形O′A′B′C′是水平放置的一个平面图形的斜二测画法画出的直观图,其中O′A′=6cm,C′D′=2cm,则原图形是( )
如图,矩形O′A′B′C′是水平放置的一个平面图形的斜二测画法画出的直观图,其中O′A′=6cm,C′D′=2cm,则原图形是( )| A. | 正方形 | B. | 矩形 | C. | 梯形 | D. | 菱形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com