
分析 通过直线l过P(1,1)可设其方程为x=my+1-m,并与双曲线方程联立,利用韦达定理及中点坐标公式可知y1+y2=2,进而计算可得结论.
解答 解:存在直线l:x=$\frac{4}{9}$y+$\frac{5}{9}$满足题意.
理由如下:
依题意,直线l过P(1,1),则
可设直线l方程为:x=my+1-m,
联立直线l与双曲线方程,消去x整理得:
(9m2-4)y2+18m(1-m)y+9(1-m)2-36=0,
设直线l与双曲线的交点分别为A(x1,y1),B(x2,y2),
又∵弦AB的中点为P(1,1),
∴y1+y2=$\frac{18m(m-1)}{9{m}^{2}-4}$=2,
解得:m=$\frac{4}{9}$,
即存在直线l:x=$\frac{4}{9}$y+$\frac{5}{9}$,使其截双曲线所得弦的中点为P(1,1).
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:解答题
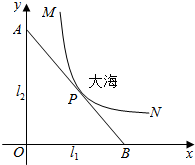 某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数$y=\frac{a}{x}$图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.
如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 35 | B. | 70 | C. | 80 | D. | 140 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
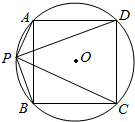 已知:如图,⊙O是正方形ABCD的外接圆,P是$\widehat{AB}$上的一点,求证:$\frac{PA+PC}{PB+PD}$=$\frac{PD}{PC}$.
已知:如图,⊙O是正方形ABCD的外接圆,P是$\widehat{AB}$上的一点,求证:$\frac{PA+PC}{PB+PD}$=$\frac{PD}{PC}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com