
【题目】某群体的人均通勤时间,是指单日内该群体成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]() 的成员自驾时,自驾群体的人均通勤时间是
的成员自驾时,自驾群体的人均通勤时间是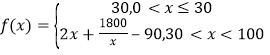 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为40钟,根据上述分析结果回答下列问题:
影响,恒为40钟,根据上述分析结果回答下列问题:
(1)请你说明,当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;讨论
的表达式;讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由题意知求出f(x)>40时x的取值范围即可;
(2)分段求出g(x)的解析式,判断g(x)的单调性,再说明其实际意义
由题意知,
当0<x![]() 30时,f(x)=30<40, 公交群体的人均通勤时间恒大于自驾群体的人均通勤时间;
30时,f(x)=30<40, 公交群体的人均通勤时间恒大于自驾群体的人均通勤时间;
当30<x<100时,![]() >40,
>40,
即x2-65x+900>0,解得x<20(舍去)或x>45
∴ 当x∈(45,100)时,公交群体的人均通勤时间少于自驾群体的人均通勤时间.
(2)当0<x≤30时,g(x)=30x%+40(1-x%)=40-![]()
当30<x<100时,![]() ;
;
∴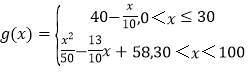
∵当0<x≤30时, g(x)=40-![]() 是单调递减函数,g(30)=37,
是单调递减函数,g(30)=37,
当30<x<100时,![]()
![]() ,且g(30)=37,
,且g(30)=37,
∴当0<x<32.5时,g(x)单调递减;当32.5<x<100时,g(x)单调递增;
实际意义:说明该地上班族S中小于32.5%的人自驾时,随着自驾占比增大,人均通勤时间是递减的;大于32.5%的人自驾时,随着自驾占比增大,人均通勤时间是递增的;当自驾人数为32.5%时,人均通勤时间最短


科目:高中数学 来源: 题型:
【题目】某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件。已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产某款手机的年固定成本为40万元,每生产1万只还需另投入16万元.设该公司一年内共生产该款手机![]() 万只并全部销售完,每万只的销售收入为
万只并全部销售完,每万只的销售收入为![]() 万元,且
万元,且
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万只)的函数解析式;
(万只)的函数解析式;
(2)当年产量为多少万只时,该公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,如果同时满足以下三条:①对任意的
,如果同时满足以下三条:①对任意的![]() ,总有
,总有![]() ;②
;②![]() ;③若
;③若![]() ,都有
,都有![]() 成立,则称函数
成立,则称函数![]() 为理想函数.
为理想函数.
(1) 若函数![]() 为理想函数,求
为理想函数,求![]() 的值;
的值;
(2)判断函数![]()
![]() 是否为理想函数,并予以证明;
是否为理想函数,并予以证明;
(3) 若函数![]() 为理想函数,
为理想函数,![]() 假定
假定![]()
![]() ,使得
,使得![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com