
【题目】已知函数{an}:a1=t,n2Sn+1=n2(Sn+an)+an2 , n=1,2,….
(1)设{an}为等差数列,且前两项和S2=3,求t的值;
(2)若t= ![]() ,证明:
,证明: ![]() ≤an<1.
≤an<1.
【答案】
(1)解:设等差数列公差为d,则2t+d=3,
又 ![]() ,
,
得a1=1或a1=﹣3,
但当a1=﹣3时,d=9,无法使 ![]() 恒成立,
恒成立,
∴t=1.
(2)解:先证an<1.
易知an>0, ![]() ,故{an}为递增数列,
,故{an}为递增数列,
从而 ![]() ,
,
∴ ![]() 有
有 ![]() ,
,
由叠加法有 ![]() (n≥2),
(n≥2),
注意到 ![]() (k≥2),
(k≥2),
∴ ![]() ,
, ![]() =
= ![]()
从而 ![]() ,即an<1(n≥2),
,即an<1(n≥2),
又 ![]() ,有an<1(n∈N*)成立.
,有an<1(n∈N*)成立.
再证 ![]() ,
,
当n=1时, ![]() 成立,
成立,
由an<1, ![]() ,
,
从而 ![]()
![]() =
= ![]()
∴ ![]() ,即有
,即有 ![]() ,
,
叠加有 ![]() (n≥2),
(n≥2),
又 ![]() ,
,
从而 ![]()
![]() =
= ![]()
∴ ![]() ,即有
,即有 ![]() (n≥2),
(n≥2),
综上 ![]() (n∈N*).
(n∈N*).
【解析】(1)利用等差数列的通项公式即可得出;(2)先证an<1.易知an>0,且{an}为递增数列,利用递推关系可得: ![]() ,利用“累加求和”方法即可证明.再证
,利用“累加求和”方法即可证明.再证 ![]() ,当n=1时,
,当n=1时, ![]() 成立,由an<1,可得:
成立,由an<1,可得: ![]() ,利用“累加求和”方法即可得出.
,利用“累加求和”方法即可得出.
【考点精析】认真审题,首先需要了解等差数列的通项公式(及其变式)(通项公式:![]() 或
或![]() ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分14分)已知递增等差数列![]() 中的
中的![]() 是函数
是函数![]() 的两个零点.数列
的两个零点.数列![]() 满足,点
满足,点![]() 在直线
在直线![]() 上,其中
上,其中![]() 是数列
是数列![]() 的前
的前![]() 项和.
项和.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半径为5的圆的圆心在![]() 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线![]() 相切.
相切.
(1)求圆的方程;
(2)设直线![]() 与圆相交于
与圆相交于![]() 、
、![]() 两点,求实数
两点,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,是否存在实数![]() ,使得弦
,使得弦![]() 的垂直平分线
的垂直平分线![]() 过点
过点![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每车每次租时间不超过两小时免费,超过两个小时的部分每小时收费2元(不足1小时的部分按1小时计算).有甲、乙两人独立来该租车点骑游(各组一车一次).设甲、乙不超过两小时还车的概率分别为![]() ,
, ![]() ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为![]() ,
, ![]() ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(1)求甲、乙两人所付租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角三角形ABC中角A,B,C对边长分别为a,b,c,∠C=90°.
(1)若三角形面积为2,求斜边长c最小值;
(2)试比较an+bn与cn(n∈N*)的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是89.
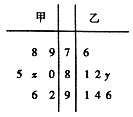
(1)求![]() 和
和![]() 的值;
的值;
(2)计算乙班7位学生成绩的方差![]() .
.
(3)从成绩在90分以上的学生中随机抽取两名学生,求乙班至少有一名学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是等腰三角形,
是等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点.
上一点.
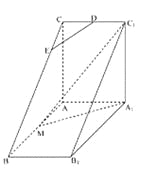
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A= ![]() ,b2﹣a2=
,b2﹣a2= ![]() c2 .
c2 .
(1)求tanC的值;
(2)若△ABC的面积为3,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com