
【题目】已知:以点C(t, ![]() )(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
)(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)当t=2时,求圆C的方程;
(2)求证:△OAB的面积为定值;
(3)设直线y=﹣2x+4与圆C交于点M,N,若|OM|=|ON|,求圆C的方程.
【答案】
(1)解:当t=2时,圆心为C(2,1),
∴圆C的方程为(x﹣2)2+(y﹣1)2=5;
(2)证明:由题设知,圆C的方程为(x﹣t)2+(y﹣ ![]() )2=t2+
)2=t2+ ![]() ,
,
化简得x2﹣2tx+y2﹣ ![]() y=0.
y=0.
当y=0时,x=0或2t,则A(2t,0);
当x=0时,y=0或 ![]() ,则B(0,
,则B(0, ![]() ),
),
∴S△AOB= ![]() OAOB=
OAOB= ![]() |2t||
|2t|| ![]() |=4为定值.
|=4为定值.
(3)解:∵OM=ON,则原点O在MN的中垂线上,设MN的中点为H,则CH⊥MN,
∴C、H、O三点共线,KMN=﹣2,则直线OC的斜率k= ![]() ,
,
∴t=2或t=﹣2.
∴圆心为C(2,1)或C(﹣2,﹣1),
∴圆C的方程为(x﹣2)2+(y﹣1)2=5或(x+2)2+(y+1)2=5.
由于当圆方程为(x+2)2+(y+1)2=5时,直线2x+y﹣4=0到圆心的距离d>r,
此时不满足直线与圆相交,故舍去,
∴所求的圆C的方程为(x﹣2)2+(y﹣1)2=5.
【解析】(1)当t=2时,圆心为C(2,1),即可得出圆C的方程;(2)求出半径,写出圆的方程,再解出A、B的坐标,表示出面积即可;(3)设MN的中点为H,则CH⊥MN,根据C、H、O三点共线,KMN=﹣2,由直线OC的斜率k= ![]() ,求得t的值,可得所求的圆C的方程.
,求得t的值,可得所求的圆C的方程.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示. 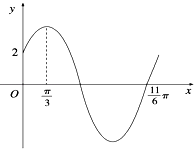
(1)求f(x)的解析式;
(2)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的 ![]() 倍,再将所得函数图象向右平移
倍,再将所得函数图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
(3)当x∈[﹣ ![]() ,
, ![]() ]时,求函数y=f(x+
]时,求函数y=f(x+ ![]() )﹣
)﹣ ![]() f(x+
f(x+ ![]() )的最值.
)的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1)所示,已知四边形![]() 是由直角△
是由直角△![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]()
![]() .且点
.且点![]() 为线段
为线段![]() 的中点,
的中点, ![]() ,
, ![]() 现将△
现将△![]() 沿
沿![]() 进行翻折,使得二面角
进行翻折,使得二面角![]()
![]() 的大小为
的大小为![]() ,得到图形如图(2)所示,连接
,得到图形如图(2)所示,连接![]() ,点
,点![]() 分别在线段
分别在线段![]() 上.
上.


(1)证明: ![]() ;
;
(2)若三棱锥![]() 的体积为四棱锥
的体积为四棱锥![]() 体积的
体积的![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个古典型(或几何概型)中,若两个不同随机事件![]() 、
、![]() 概率相等,则称
概率相等,则称![]() 和
和![]() 是“等概率事件”,如:随机抛掷一枚骰子一次,事件“点数为奇数”和“点数为偶数”是“等概率事件”,关于“等概率事件”,以下判断正确的是__________.
是“等概率事件”,如:随机抛掷一枚骰子一次,事件“点数为奇数”和“点数为偶数”是“等概率事件”,关于“等概率事件”,以下判断正确的是__________.
①在同一个古典概型中,所有的基本事件之间都是“等概率事件”;
②若一个古典概型的事件总数为大于2的质数,则在这个古典概型中除基本事件外没有其他“等概率事件”;③因为所有必然事件的概率都是1,所以任意两个必然事件是“等概率事件”;
④随机同时抛掷三枚硬币一次,则事件“仅有一个正面”和“仅有两个正面”是“等概率事件”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处有极小值
处有极小值![]() ,求
,求![]() ,
,![]() 的值;
的值;
(Ⅱ)若![]() ,设
,设![]() ,求证:当
,求证:当![]() 时,
时,![]() ;
;
(Ⅲ)若![]() ,
,![]() ,对于给定
,对于给定![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,若
,若![]() .求
.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点在
的焦点在![]() 轴上,且椭圆
轴上,且椭圆![]() 的焦距为2.
的焦距为2.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,过
,过![]() 作
作![]() 轴且与椭圆
轴且与椭圆![]() 交于另一点
交于另一点![]() ,
, ![]() 为椭圆
为椭圆![]() 的右焦点,求证:三点
的右焦点,求证:三点![]() 在同一条直线上.
在同一条直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】完成下列进位制之间的转化.
(1)10231(4)=________(10);
(2)235(7)=________(10);
(3)137(10)=________(6);
(4)1231(5)=________(7);
(5)213(4)=________(3);
(6)1010111(2)=________(4).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com