
【题目】已知函数f(x)= ![]() ,直线y=
,直线y= ![]() x为曲线y=f(x)的切线(e为自然对数的底数).
x为曲线y=f(x)的切线(e为自然对数的底数).
(1)求实数a的值;
(2)用min{m,n}表示m,n中的最小值,设函数g(x)=min{f(x),x﹣ ![]() }(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
}(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
【答案】
(1)解:函数f(x)= ![]() 的导数为f′(x)=
的导数为f′(x)= ![]() ,
,
设切点为(m,n),即有n= ![]() ,n=
,n= ![]() m,
m,
可得ame=em,①
由直线y= ![]() x为曲线y=f(x)的切线,可得
x为曲线y=f(x)的切线,可得
![]() =
= ![]() ,②
,②
由①②解得m=1,a=1
(2)解:函数g(x)=min{f(x),x﹣ ![]() }(x>0),
}(x>0),
由f(x)= ![]() 的导数为f′(x)=
的导数为f′(x)= ![]() ,
,
当0<x<2时,f(x)递增,x>2时,f(x)递减.
对x﹣ ![]() 在x>0递增,设y=f(x)和y=x﹣
在x>0递增,设y=f(x)和y=x﹣ ![]() 的交点为(x0,y0),
的交点为(x0,y0),
由f(1)﹣(1﹣1)= ![]() >0,f(2)﹣(2﹣
>0,f(2)﹣(2﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() <0,即有1<x0<2,
<0,即有1<x0<2,
当0<x<x0时,g(x)=x﹣ ![]() ,
,
h(x)=g(x)﹣cx2=x﹣ ![]() ﹣cx2,h′(x)=1+
﹣cx2,h′(x)=1+ ![]() ﹣2cx,
﹣2cx,
由题意可得h′(x)≥0在0<x<x0时恒成立,
即有2c≤ ![]() +
+ ![]() ,由y=
,由y= ![]() +
+ ![]() 在(0,x0)递减,
在(0,x0)递减,
可得2c≤ ![]() +
+ ![]() ①
①
当x≥x0时,g(x)= ![]() ,
,
h(x)=g(x)﹣cx2= ![]() ﹣cx2,h′(x)=
﹣cx2,h′(x)= ![]() ﹣2cx,
﹣2cx,
由题意可得h′(x)≥0在x≥x0时恒成立,
即有2c≤ ![]() ,由y=
,由y= ![]() ,可得y′=
,可得y′= ![]() ,
,
可得函数y在(3,+∞)递增;在(x0,3)递减,
即有x=3处取得极小值,且为最小值﹣ ![]() .
.
可得2c≤﹣ ![]() ②,
②,
由①②可得2c≤﹣ ![]() ,解得c≤﹣
,解得c≤﹣ ![]() .
.
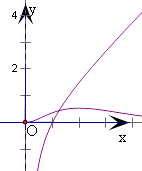
【解析】(1)求出f(x)的导数,设出切点(m,n),可得切线的斜率,由切线方程可得a,m的方程,解方程可得a=1;(2)y=f(x)和y=x﹣ ![]() 的交点为(x0 , y0),分别画出y=f(x)和y=x﹣
的交点为(x0 , y0),分别画出y=f(x)和y=x﹣ ![]() 在x>0的图象,可得1<x0<2,再由新定义求得最小值,求得h(x)的解析式,由题意可得h′(x)≥0在0<x<x0时恒成立,运用参数分离和函数的单调性,即可得到所求c的范围.
在x>0的图象,可得1<x0<2,再由新定义求得最小值,求得h(x)的解析式,由题意可得h′(x)≥0在0<x<x0时恒成立,运用参数分离和函数的单调性,即可得到所求c的范围.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|2x﹣a|﹣1.
①当a=0时,不等式f(x)+1>0的解集为_____;
②若函数f(x)有三个不同的零点,则实数a的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分位于正方形的中心成中心对称,在正方形内随机取一点,则此点取自黑色部分的概率是( )
内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分位于正方形的中心成中心对称,在正方形内随机取一点,则此点取自黑色部分的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级某次数学竞赛随机抽取100名学生的成绩,分组为[50,60),[60,70),[70,80),[80,90),[90,100],统计后得到频率分布直方图如图所示:

(1)试估计这组样本数据的众数和中位数(结果精确到0.1);
(2)年级决定在成绩[70,100]中用分层抽样抽取6人组成一个调研小组,对高一年级学生课外学习数学的情况做一个调查,则在[70,80),[80,90),[90,100]这三组分别抽取了多少人?
(3)现在要从(2)中抽取的6人中选出正副2个小组长,求成绩在[80,90)中至少有1人当选为正、副小组长的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中_________为真命题.
①“A∩B=A”成立的必要条件是“A![]() B”; w ②“若x2+y2=0,则x,y全为0”的否命题;
B”; w ②“若x2+y2=0,则x,y全为0”的否命题;
③“全等三角形是相似三角形”的逆命题; ④“圆内接四边形对角互补”的逆否命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com