练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设是圆上的动点，点是在轴上的投影，且.

    （1）当在圆上运动时，求点的轨迹的方程；

    （2）求过点(1,0)，倾斜角为的直线被所截线段的长度.

    【答案】（1）（2）

    【解析】

    （1）设的坐标为,的坐标为.由,可得,可列出,坐标关系式为,即可得到的轨迹的方程.

    （2）设直线方程为:,代入椭圆方程,由韦达定理和弦长公式:,即可求得直线被C所截线段的长度.

    （1）设的坐标为,的坐标为.

    由,可得,

    的坐标为,是圆上的动点

    ┄①

    ,坐标关系式为: ┄②代入①得:

    整理可得的轨迹的方程:

    （2）求过点,倾斜角为的直线方程为:

    设直线与轨迹的交点为

    将直线方程与轨迹方程联立方程组,消掉

    得:

    整理可得:

    根据韦达定理得:

    ∴线段AB的长度为:

    所以线段AB的长度:.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知在平面直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，轴的非负半轴为极轴且取相同的单位长度建立极坐标系，圆的极坐标方程为.

    （1）求直线的普通方程以及圆的直角坐标方程；

    （2）若直线与圆交于两点，求线段的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为为抛物线上位于第一象限内的点，过点的直线交抛物线于另一点，交轴的正半轴于点．

    （1）若点的横坐标为，且与双曲线的实轴长相等，求抛物线的方程；

    （2）对于（1）中求出的抛物线，若点，记点关于轴的对称点为（不同于点），直线交轴于点．

    ①求证：点的坐标为；

    ②若，求点到直线的距离的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于函数，.有下列命题：

    ①对,恒有成立.

    ②,使得成立.

    ③“若,则有且.”的否命题.

    ④“若且,则有.”的逆否命题.

    其中，真命题有_____________.（只需填序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】上周某校高三年级学生参加了数学测试，年级组织任课教师对这次考试进行成绩分析现从中随机选取了40名学生的成绩作为样本，已知这40名学生的成绩全部在40分至100分之间，现将成绩按如下方式分成6组：第一组；第二组；……；第六组，并据此绘制了如图所示的频率分布直方图．

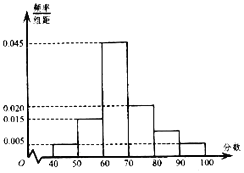
    （1）估计这次月考数学成绩的平均分和众数；

    （2）从成绩大于等于80分的学生中随机选2名，求至少有1名学生的成绩在区间内的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】据史载知，新华网：北京2008年11月9日电，国务院总理温家宝主持召开国务院常务会议，研究部署进一步扩大内需促进经济平稳较快增长的措施，以应对日趋严峻的全球性世界经济金融危机.在提高城乡居民特别是低收入人群的收入水平政策措施的刺激下，某零售店当时近5个月的销售额和利润额数据统计如下表：

    月份

    2

    3

    4

    5

    6

    销售额/千万元

    3

    5

    6

    7

    9

    利润额/千万元

    2

    3

    3

    4

    5

    （1）若与之间是线性相关关系，求利润额关于销售额的线性回归方程；

    （2）若9月份的销售额为8千万元，试利用（1）的结论估计该零售店9月份的利润额.

    参考公式：，.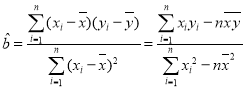

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点.

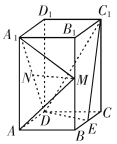
    （1）证明：MN∥平面C1DE；

    （2）求点C到平面C1DE的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，，.

    （1）若，求的值；

    （2）当，，且有最小值时，求的值；

    （3）当，时，有恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】 设椭圆的左焦点为，左顶点为，顶点为B.已知（为原点）.

    （Ⅰ）求椭圆的离心率；

    （Ⅱ）设经过点且斜率为的直线与椭圆在轴上方的交点为，圆同时与轴和直线相切，圆心在直线上，且，求椭圆的方程.

    查看答案和解析>>

    同步练习册答案