【题目】已知两平行直线4x﹣2y+7=0，2x﹣y+1=0之间的距离等于坐标原点O到直线l：x﹣2y+m=0的距离的一半．
（1）求m的值；
（2）判断直线l与圆 
的位置关系．
【答案】
（1）解：2x﹣y+1=0化为4x﹣2y+2=0，
则两平行直线4x﹣2y+7=0，2x﹣y+1=0之间的距离等于 
= 
，
∴点O到直线l：x﹣2y+m=0（m＞0）的距离= 
= 
，
∵m＞0
∴m=5
（2）解：圆C：x2+（y﹣2）2= 
的圆心C（0，2），半径r= 
，
∵C到直线l的距离d= 
= ，
∴l与圆C相切
【解析】（1）求出两平行直线4x﹣2y+7=0，2x﹣y+1=0之间的距离，利用两平行直线4x﹣2y+7=0，2x﹣y+1=0之间的距离等于坐标原点O到直线l：x﹣2y+m=0（m＞0）的距离的一半，建立方程，即可求m的值；（2）求出C到直线l的距离，即可得出结论．
科目：高中数学 来源： 题型：
【题目】某次大型运动会的组委会为了搞好接待工作，招募了16名男志愿者和14名女志愿者，调查发现，男、女志愿者中分别有10人和6人喜爱运动，其余人不喜爱运动．
（1）根据以上数据完成下面2×2列联表：
喜爱运动 | 不喜爱运动 | 总计 | |
男 | 10 | 16 | |
女 | 6 | 14 | |
总计 | 30 |
（2）能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关系？
（3）已知喜欢运动的女志愿者中恰有4人会外语，如果从中抽取2人负责翻译工作，那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少？
参考公式：K2= 
，其中n=a+b+c+d．
参考数据：
P（K2≥k0） | 0.40 | 0.25 | 0.10 | 0.010 |
k0 | 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设 
，曲线y=f（x）在点（1，f（1））处的切线与直线2x+y+1=0垂直．
（1）求a的值；
（2）若x∈[1，+∞），f（x）≤m（x﹣1）恒成立，求m的范围．
（3）求证： 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】近几年，电商行业的蓬勃发展也带动了快递业的高速发展.某快递配送站每天至少要完成1800件包裹的配送任务，该配送站有8名新手快递员和4名老快递员，但每天最多安排10人进行配送.已知每个新手快递员每天可配送240件包裹，日工资320元；每个老快递员每天可配送300件包裹，日工资520元.
(1)求该配送站每天需支付快递员的总工资最小值；
(2)该配送站规定:新手快递员某个月被评为“优秀”，则其下个月的日工资比这个月提高12%.那么新手快递员至少连续几个月被评为“优秀”，日工资会超过老快递员?
(参考数据: 
， 
， 
.)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益函数为R（x）=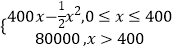 
，其中x是仪器的产量（单位：台）；
（1）将利润f（x）表示为产量x的函数（利润=总收益﹣总成本）；
（2）当产量x为多少台时，公司所获利润最大？最大利润是多少元？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为得到函数y=sin（x+ 
）的图象，可将函数y=sinx的图象向左平移m个单位长度，或向右平移n个单位长度（m，n均为正数），则|m﹣n|的最小值是（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
