
【题目】已知a,b,c是![]() ABC中角A,B,C的对边,S是
ABC中角A,B,C的对边,S是![]() ABC的面积.若a2+c2=b2+ac,
ABC的面积.若a2+c2=b2+ac,
(I)求角B ; (II)若b=2,S=![]() ,判断三角形形状
,判断三角形形状
【答案】(I)![]() ;(Ⅱ)等边三角.
;(Ⅱ)等边三角.
【解析】试题分析:
(1)利用题意首先求得![]() 的值,然后利用特殊角的三角函数值求解
的值,然后利用特殊角的三角函数值求解![]() 的大小即可;
的大小即可;
(2)利用三角形的面积公式确定![]() 即可确定△ABC为等边三角形.
即可确定△ABC为等边三角形.
试题解析:
(I)由![]() 得
得![]()
又因为![]()
所以![]()
又![]() 所以
所以![]()
(Ⅱ)![]() ,得
,得![]()
又![]() ,所以
,所以 ![]() ,得
,得![]()
故三角形为等边三角
点睛:在解三角形的问题中,三角形内角和定理起着重要作用,在解题时要注意根据这个定理确定角的范围及三角函数值的符号,防止出现增解或漏解.
正、余弦定理在应用时,应注意灵活性,尤其是其变形应用时可相互转化.如a2=b2+c2-2bccos A可以转化为sin2 A=sin2 B+sin2 C-2sin Bsin Ccos A,利用这些变形可进行等式的化简与证明.
判断三角形形状的两种途径,一是化边为角;二是化角为边,并常用正弦(余弦)定理实施边、角转换.


科目:高中数学 来源: 题型:
【题目】某校的一个社会实践调查小组,在对该校学生的良好“用眼习惯”的调查中,随机发放了120分问卷.对收回的100份有效问卷进行统计,得到如![]() 下列联表:
下列联表:
做不到科学用眼 | 能做到科学用眼 | 合计 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合计 | 75 | 25 | 100 |
(1)现按女生是否能做到科学用眼进行分层,从45份女生问卷中抽取了6份问卷,从这6份问卷中再随机抽取3份,并记其中能做到科学用眼的问卷的份数![]() ,试求随机变量
,试求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(2)若在犯错误的概率不超过![]() 的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的
的前提下认为良好“用眼习惯”与性别有关,那么根据临界值表,最精确的![]() 的值应为多少?请说明理由.
的值应为多少?请说明理由.
附:独立性检验统计量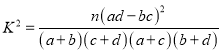 ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点 ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 与点
与点![]() 均在椭圆
均在椭圆![]() 上,且
上,且![]() 关于原点对称,问:椭圆上是否存在点
关于原点对称,问:椭圆上是否存在点![]() (点
(点![]() 在一象限),使得
在一象限),使得![]() 为等边三角形?若存在,求出点
为等边三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在10名学生中,男生有x名,现从10名学生中任选6人去参加某项活动:①至少有1名女生;②5名男生,1名女生;③3名男生,3名女生.若要使①为必然事件,②为不可能事件,③为随机事件,则x=( )
A.5B.6C.3或4D.5或6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某烟花厂家为了测试最新研制出的一种“冲天”产品升空的安全性,特对其进行了一项测试。如图,这种烟花在燃放点C进行燃放实验,测试人员甲、乙分别在A,B两地(假设三地在同一水平面上),测试人员甲测得A、B两地相距80米且∠BAC=60°,甲听到烟花燃放“冲天”时的声音的时间比乙晚![]() 秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)
秒.在A地测得该烟花升至最高点H处的仰角为60°.(已知声音的传播速度为340米∕秒)
(1)求甲距燃放点C的距离;(2)求这种烟花的垂直“冲天”高度HC

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个人连续射击三次,事件“至少有一次击中目标”的对立事件是( )
A.至多有一次击中目标B.三次都击不中目标
C.三次都击中目标D.只有一次击中目标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点
轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点![]() 与
与![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆于
交椭圆于![]() 两点.
两点.
(1)求椭圆的方程;
(2)当直线![]() 的斜率为1时,求
的斜率为1时,求![]() 的面积;
的面积;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形?若存在,求出
为邻边的平行四边形是菱形?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com