Question

【题目】如图所示，四边形ABCD为矩形，AD⊥平面ABE，AE=EB=BC，F为CE上的点，且BF⊥平面ACE．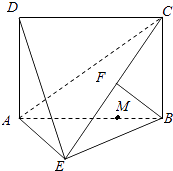
（1）求证：AE⊥BE；
（2）设M在线段AB上，且满足AM=2MB，试在线段CE上确定一点N，使得MN∥平面DAE．

Answer 1

【答案】
（1）证明：∵BF⊥平面ACE，AE平面ACE，

∴BF⊥AE，BF⊥CE，

∵EB=BC，∴F是CE的中点，

又∵AD⊥平面ABE，AD平面ABCD，

∴平面ABCD⊥平面ABE，

∵平面ABCD∩平面ABE=AB，BC⊥AB

∴BC⊥平面ABE，

从而BC⊥AE，且BC∩BF=B，

∴AE⊥平面BCE，BE平面BCE，

∴AE⊥BE；

（2）证明：在△ABE中过M点作MG∥AE交BE于G点，

在△BEC中过G点作GN∥BC交EC于N点，连MN，

∴CN= CE．

∵MG∥AE，MG平面ADE，AE平面ADE，

∴MG∥平面ADE．

同理，GN∥平面ADE，且MG与GN交于G点，

∴平面MGN∥平面ADE．

又MN平面MGN，

∴MN∥平面ADE．

故N点为线段CE上靠近C点的一个三等分点．

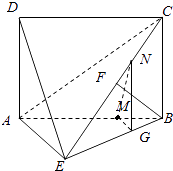
【解析】（1）由AD∥BC和AD⊥平面ABE证明AE⊥BC，再由BF⊥平面ACE得AE⊥BF，根据线面垂直的判定定理证出AE⊥平面BCE，即证出AE⊥BE；（2）在△ABE中过M点作MG∥AE交BE于G点，在△BEC中过G点作GN∥BC交EC于N点，连MN，证明平面MGE∥平面ADE，可得MN∥平面ADE，从而可得结论．
【考点精析】本题主要考查了空间中直线与直线之间的位置关系和直线与平面平行的性质的相关知识点，需要掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点；一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行才能正确解答此题．