
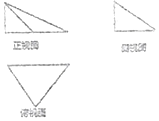
 一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )
一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,侧视图是一个直角边长为1的直角三角形,则该几何体外接球的体积是( )| A. | 36π | B. | 9π | C. | $\frac{9}{2}π$ | D. | $\frac{27}{5}π$ |
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {1} | C. | {4} | D. | {1,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 | 1014年(1-12月) | 1015年(1-12月) | 1016年(1-11月) |
| 接单量(单) | 14463272 | 40125125 | 50331996 |
| 油费(元) | 214301962 | 591305364 | 653214963 |
| 平均每单油费t(元) | 14.82 | 14.49 | |
| 平均每单里程k(公里) | 15 | 15 | |
| 每公里油耗a(元) | 0.7 | 0.7 | 0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
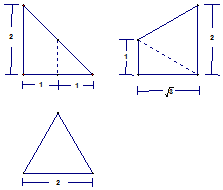 如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )
如图是某空间几何体的三视图其中主视图、侧视图、俯视图依次为直角三角形、直角梯形、等边三角形,则该几何体的体积( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
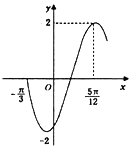 函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.
函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<ω<\frac{π}{2}})$的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为y=2sin2x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com