
已知四棱锥P?ABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点.
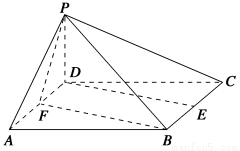
(1)求证:DE∥平面PFB;
(2)已知二面角P?BF?C的余弦值为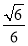 ,求四棱锥P?ABCD的体积.
,求四棱锥P?ABCD的体积.
(1)见解析(2)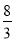
【解析】(1)因为E,F分别为正方形ABCD的两边BC,AD的中点,所以BE綉FD,即BEDF为平行四边形,
∴ED∥FB,∵FB?平面PFB,且ED?平面PFB,
∴DE∥平面PFB.
(2)以D为原点,直线DA,DC,DP分别为x,y,z轴建立空间直角坐标系.如图,设PD=a,
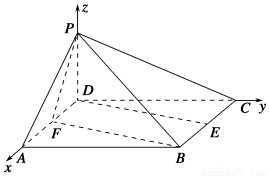
可得如下点的坐标P(0,0,a),F(1,0,0),B(2,2,0).
则有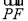 =(1,0,-a),
=(1,0,-a), =(1,2,0).
=(1,2,0).
因为PD⊥底面ABCD,所以平面ABCD的一个法向量为m=(0,0,1).
设平面PFB的法向量为n=(x,y,z),
则可得 即
即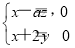 .,
.,
令x=1, 得z=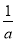 ,y=-
,y=-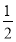 ,
,
所以n=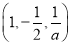 .
.
由已知二面角P-BF-C的余弦值为 ,
,
所以得cos〈m,n〉=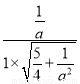 =
=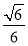 ,
,
∴a=2,∴VP-ABCD=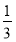 ×2×2×2=
×2×2×2=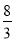


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练18练习卷(解析版) 题型:选择题
记△ABC各边的中点分别为D,E,F,在A,B,C,D,E,F中任取4点,若这4点为平行四边形顶点,则称为选取成功.某人连续进行3次这种选取,则至少成功1次的概率是( ).
A.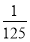 B.
B. C.
C.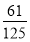 D.
D.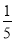
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:填空题
若直线l:4x+3y-8=0过圆C:x2+y2-ax=0的圆心且交圆C于A,B两点,O坐标原点,则△OAB的面积为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:选择题
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )
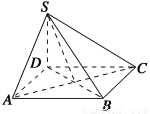
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:选择题
如图所示,在四边形A-BCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A?BCD,则在三棱锥ABCD中,下列命题正确的是( ).

A.平面ABD⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ADC⊥平面ABC
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练11练习卷(解析版) 题型:填空题
如图,在三棱柱A1B1C1?ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F?ADE的体积为V1,三棱柱A1B1C1?ABC的体积为V2,则V1∶V2=________.
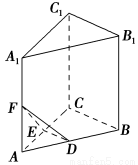
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:解答题
已知函数f(x)=(x-1)2,g(x)=4(x-1),数列{an}是各项均不为0的等差数列,其前n项和为Sn,点(an+1,S2n-1)在函数f(x)的图象上;数列{bn}满足b1=2,bn≠1,且(bn-bn+1)·g(bn)=f(bn)(n∈N+).
(1)求an并证明数列{bn-1}是等比数列;
(2)若数列{cn}满足cn=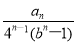 ,证明:c1+c2+c3+…+cn<3.
,证明:c1+c2+c3+…+cn<3.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷5练习卷(解析版) 题型:填空题
已知直线y=a交抛物线y=x2于A,B两点.若该抛物线上存在点C,使得∠ACB为直角,则a的取值范围为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷2练习卷(解析版) 题型:解答题
已知向量a=(Asin ωx,Acos ωx),b=(cos θ,sin θ),f(x)=a·b+1,其中A>0,ω>0,θ为锐角.f(x)的图象的两个相邻对称中心的距离为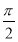 ,且当x=
,且当x=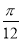 时,f(x)取得最大值3.
时,f(x)取得最大值3.
(1)求f(x)的解析式;
(2)将f(x)的图象先向下平移1个单位,再向左平移φ(φ>0)个单位得g(x)的图象,若g(x)为奇函数,求φ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com