
| A. | $\frac{16}{3}$ | B. | 16 | C. | 8 | D. | $\frac{{16\sqrt{3}}}{3}$ |
分析 求出直线方程,直线方程与抛物线方程联立,利用弦长公式求解即可.
解答 解:直线$l:y=\frac{{\sqrt{3}}}{3}x+1$与x2=4y联立得${x^2}-\frac{{4\sqrt{3}}}{3}x-4=0$,$△=\frac{64}{3}$,
x1+x2=$\frac{4\sqrt{3}}{3}$,x1x2=-4
故$|{AB}|=\sqrt{1+{k^2}}•|{{x_1}-{x_2}}|=\sqrt{1+\frac{1}{3}}•\frac{8}{{\sqrt{3}}}=\frac{16}{3}$,
故选:A.
点评 本题考查直线与抛物线的位置关系的应用,考查计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
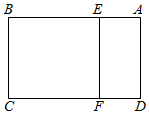 如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )
如图,在矩形ABCD中,AD=$\sqrt{5}$,AB=3,E、F分别为AB边、CD边上一点,且AE=DF=l,现将矩形ABCD沿EF折起,使得平面ADFE⊥平面BCFE,连接AB、CD,则所得三棱柱ABE-DCF的侧面积比原矩形ABCD的面积大约多(取$\sqrt{5}$≈2.236)( )| A. | 68% | B. | 70% | C. | 72% | D. | 75% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(6,±6\sqrt{2})$ | B. | $(6\sqrt{2},±6)$ | C. | $(12,±6\sqrt{2})$ | D. | $(6\sqrt{2},±12)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0}⊆M | B. | M=∅ | C. | -1∈M | D. | 2∈M |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com