
【题目】把半椭圆![]() (
(![]() )与圆弧
)与圆弧![]() (
(![]() )合成的曲线称作“曲圆”,其中
)合成的曲线称作“曲圆”,其中![]() 为
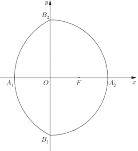
为![]() 的右焦点,如图所示,
的右焦点,如图所示,![]() 、
、![]() 、
、![]() 、
、![]() 分别是“曲圆”与
分别是“曲圆”与![]() 轴、
轴、![]() 轴的交点,已知
轴的交点,已知![]() ,过点
,过点![]() 且倾斜角为
且倾斜角为![]() 的直线交“曲圆”于
的直线交“曲圆”于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 轴的上方).
轴的上方).
(1)求半椭圆![]() 和圆弧
和圆弧![]() 的方程;
的方程;
(2)当点![]() 、
、![]() 分别在第一、第三象限时,求△
分别在第一、第三象限时,求△![]() 的周长
的周长![]() 的取值范围;
的取值范围;
(3)若射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 交“曲圆”于点
交“曲圆”于点![]() ,请用
,请用![]() 表示
表示![]() 、
、![]() 两点的坐标,并求△
两点的坐标,并求△![]() 的面积的最小值.
的面积的最小值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,设直线
,设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,![]() 为线段
为线段![]() 的中点.
的中点.

(1)若直线![]() 的倾斜角为
的倾斜角为![]() ,求
,求![]() 的值;
的值;
(2)设直线![]() 交直线
交直线![]() 于点
于点![]() ,证明:直线
,证明:直线![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十七世纪,法国数学家费马提出猜想;“当整数![]() 时,关于
时,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 没有正整数解”,经历三百多年,1995年英国数学家安德鲁
没有正整数解”,经历三百多年,1995年英国数学家安德鲁![]() 怀尔斯给出了证明,使它终成费马大定理,则下面命题正确的是( )
怀尔斯给出了证明,使它终成费马大定理,则下面命题正确的是( )
①对任意正整数![]() ,关于
,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 都没有正整数解;
都没有正整数解;
②当整数![]() 时,关于
时,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 至少存在一组正整数解;
至少存在一组正整数解;
③当正整数![]() 时,关于
时,关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 至少存在一组正整数解;
至少存在一组正整数解;
④若关于![]() 、
、![]() 、
、![]() 的方程
的方程![]() 至少存在一组正整数解,则正整数
至少存在一组正整数解,则正整数![]() ;
;
A.①②/span>B.①③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() (
(![]() ),定点
),定点![]() ,
,![]() ,其中
,其中![]() 为正实数.
为正实数.
(1)当![]() 时,判断直线
时,判断直线![]() 与圆
与圆![]() 的位置关系;
的位置关系;
(2)当![]() 时,若对于圆
时,若对于圆![]() 上任意一点
上任意一点![]() 均有
均有![]() 成立(
成立(![]() 为坐标原点),求实数
为坐标原点),求实数![]() 的值;
的值;
(3)当![]() 时,对于线段
时,对于线段![]() 上的任意一点
上的任意一点![]() ,若在圆
,若在圆![]() 上都存在不同的两点
上都存在不同的两点![]() ,使得点
,使得点![]() 是线段
是线段![]() 的中点,求实数
的中点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有9个大小形状完全相同的球,球的编号分别为1,2,…,9,随机摸出两个球,则两个球的编号之和大于9的概率是______(结果用分数表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司对4月份员工的奖金情况统计如下:
奖金(单位:元) | 8000 | 5000 | 4000 | 2000 | 1000 | 800 | 700 | 600 | 500 |
员工(单位:人) | 1 | 2 | 4 | 6 | 12 | 8 | 20 | 5 | 2 |
根据上表中的数据,可得该公司4月份员工的奖金:①中位数为800元;②平均数为1373元;③众数为700元,其中判断正确的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com